Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Gọi trung tuyến ứng với cạnh BC là AM
Giả sử AB < AC
Xét \(\Delta\)AMB và \(\Delta\)AMC có
AM: cạnh chung
BM = CM (gt)
AB < AC (điều giả sử)
Do đó ^AMB < ^AMC
Tiếp tục xét \(\Delta\)GMB và \(\Delta\)GMC có:
GM: cạnh chung
BM = MC (gt)
^AMB < ^AMC (cmt)
Do đó BG < CG
Kết hợp với AB < AC (gt) suy ra AB + BG < AC + CG (trái với gt)
Tương tự AB > AC cũng là điều sai
Vậy AB = AC hay \(\Delta\)ABC cân tại A (đpcm)
Gọi trung tuyến ứng với cạnh BC là AM
Giả sử AB < AC
Xét ΔAMB và ΔAMC có
AM: cạnh chung
BM = CM (gt)
AB < AC (điều giả sử)
Do đó ^AMB < ^AMC
Tiếp tục xét ΔGMB và ΔGMC có:
GM: cạnh chung
BM = MC (gt)
^AMB < ^AMC (cmt)
Do đó BG < CG
Kết hợp với AB < AC (gt) suy ra AB + BG < AC + CG (trái với gt)
Tương tự AB > AC cũng là điều sai
Vậy AB = AC hay ΔABC cân tại A (đpcm)

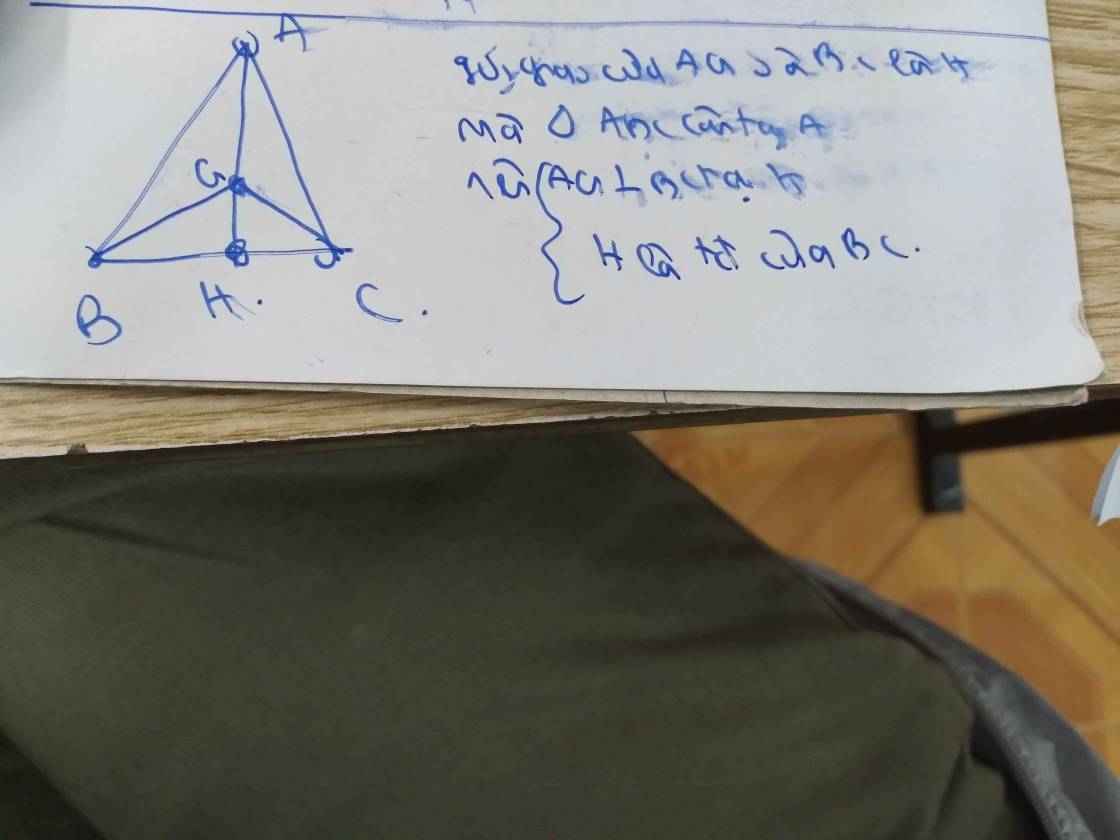
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó; ΔAHB=ΔAHC
b: Xét ΔABC có
AH là đường trung tuyến
AG=2/3AH
Do đó: G là trọng tâm
=>M là trung điểm của AC
c: Vì G là trọng tâm của ΔABC
mà N là trung điểm của AB
nên C,G,Nthẳng hàng

A B C G M
Giải:
a, Ta có: \(AB^2+AC^2=6^2+8^2=100\)
\(BC^2=100\)
\(\Rightarrow AB^2+AC^2=BC^2\)
\(\Rightarrow\Delta ABC\) vuông tại A ( đpcm )
b, \(\Delta ABC\) vuông tại A có AM là trung tuyến
\(\Rightarrow AM=\dfrac{1}{2}BC\Rightarrow AM=5\)
Mà \(AG=\dfrac{2}{3}.AM\Rightarrow AG=\dfrac{10}{3}\left(cm\right)\)
Vậy...