cho tam giác abc cân tại a có ab=ac=10cm bc=8cm gọi g là trọng tâm của tam giác abc tính ag,bg,cg

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

hieu

23 tháng 3 2023

cho tam giác abc cân tại a có ab=ac=10cm bc=8cm gọi g là trọng tâm của tam giác abc tính ag,bg,cg

#Toán lớp 7

Nguyễn Lê Phước Thịnh

23 tháng 3 2023

Đúng(2)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Mitt

28 tháng 12 2021

Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Kẻ đường trung tuyến AM, BN, CQ. G là trọng tâm của tam giác ABC. Tính AG, BG, CG.

#Toán lớp 7

Nguyễn Lê Phước Thịnh

29 tháng 12 2021

AG=10/3(cm)

Đúng(0)

Mai Phương Nguyễn

15 tháng 5 2022

Cho tam giác ABC cân tại A, đường cao AH. Gọi G là trọng tâm tam giác ABC. Trên tia đối của tia HG lấy điểm E sao cho HG=EH

a, Chứng minh BG=CG=BC=CE

b, Chứng minh AG=GE

c, Biết AH=9cm, BC=8cm. Tính BE, AB

d, Tam giác ABC thỏa mãn điều kiện gì để tam giác GBE là tam giác đều

#Toán lớp 7

Nguyễn Lê Phước Thịnh

15 tháng 5 2022

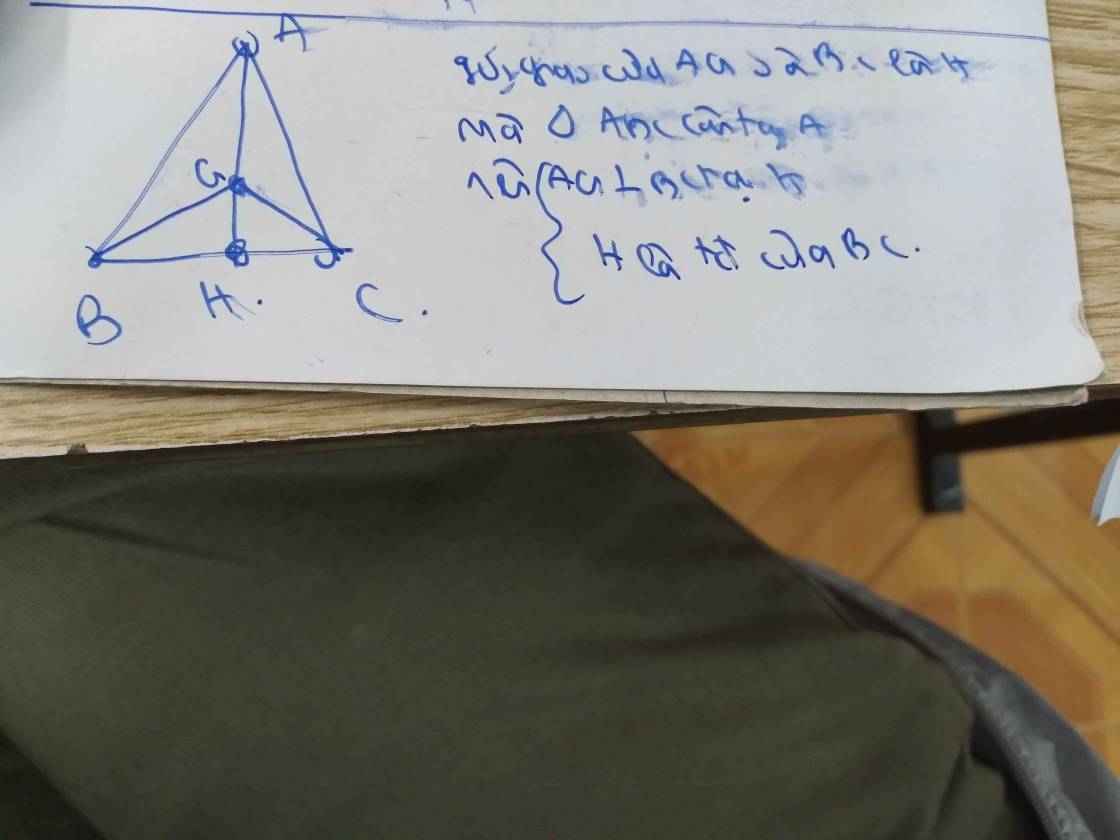
a: Xét tứ giác BGCE có

H là trung điểm của BC

H là trung điểm của GE

Do đó; BGCE là hình bình hành

mà GE⊥CB

nên BGCE là hình thoi

=>BG=GC=CE=BE

b: Ta có: AG=2GH

mà GE=2GH

nên GA=GE

c: BC=8cm nên BH=4(cm)

\(AB=\sqrt{9^2+4^2}=\sqrt{97}\left(cm\right)\)

Đúng(3)

Nguyen Le Ha Chi

14 tháng 4 2017 - olm

Cho tam giác ABC cân tại A, đường cao AH. Gọi G là trọng tâm tam giác ABC. Trên tia đối của tia HG lấy điểm E sao cho HG=EH

a, Chứng minh BG=CG=BC=CE

b, Chứng minh AG=GE

c, Biết AH=9cm, BC=8cm. Tính BE, AB

d, Tam giác ABC thỏa mãn điều kiện gì để tam giác GBE là tam giác đều

Giúp mình nhanh nha!

#Toán lớp 7

Trần Đình Hòa

18 tháng 4 2016 - olm

Cho tam giác ABC cân tại A, Đường cao AH. G là trọng tâm của tam giác ABC. Trên tia đối của HG lấy E sao cho GH=EH

a) CM BG=CG=BE=CE

b)tam giác ABE=ACE

c)AG=GE

d) Biết AH=9cm, BC=8cm. Tính BE,AB

e) Tam giác thỏa mãn điều kiện gì để tam giác GBE là tam giác đều

#Toán lớp 7

thientytfboys

18 tháng 4 2016

a, + Xét tg HBG và tg HCG vuông tại H

Có : HG cạnh chung

Mà : AH là đường cao trong tg cân nên :

AH là đường trung tuyến và là đường fan giác

=> BH=HC (vì AH là đường trung tuyến)

Nên: tg HBG=HCG (ch-cgv)

Vậy : BG=GC ( 2 cạnh tương ứng ) (1)

+ Xét tg BHE và tg HCE vuông tại H

Có : HE cạnh chung

BH=HC

Nên : tg BHE= tg HCE (ch-cgv)

Vậy : BE=EC (2 cạnh tương ứng ) (2)

+Xét tg HGC và tg HCE vuông tại H

Có : HC cạnh chung

HG=HE

Nên : tg HGC=tg HCE

Vậy : GC=ce (2 cạnh tương ứng) (3)

+Xét tg BHG và tg BHE vuông tại H

BH cạnh chung

HG=HE

nên : tg BHG = tg BHE

Vậy : BG=BE ( 2 cạnh tương ứng ) (4)

Từ (1)(2)(3) và (4) suy ra :BG=CG=BE=CE

b,Xét tg ABE và tg ACE

Có : AB= AC ( tg ABC cân tại A)

BE=EC( cmt)

AE cạnh chung

Vậy : tg ABE = tg ACE (ccc)

c, k bt

d, k bt

e, Trong tg GBE có :

BG=BE

Mà trong tam giác có 2 cạnh bằng nhau thì tg đó là tg cân hoặc đều

Nên : tg GBE là tg đều .

Vậy : đpcm

Đúng(1)

thientytfboys

18 tháng 4 2016

Đúng(0)

Nguyễn Đình Lê Bảo

16 tháng 3 2023 - olm

Cho tam giác ABC vuông tại A, có AM là đường trung tuyến (M thuộc BC).Biết AB=6cm, AC=8cm. Gọi G là trọng tâm của tam guacs ABC. Tính AG, =(( cần người giúp

#Toán lớp 7

Khả Hân

23 tháng 4 2018 - olm

Cho tam giác ABC cân tại A, trung tuyến AM,AB= 12cm Bc= 10cm, G là trọng tâm của tam giác ABC. Tính AG?

#Toán lớp 7

Nguyễn Trường Hải

23 tháng 5 2020 - olm

Cho tam giác ABC cân tại A. Gọi H là trung điểm của BC

a)Chứng minh tam giác AHB= tam giác AHC

b)Qua H kẻ đường thẳng song song với AB cắt AC tại K. Chứng minh tam giác KHC và tam giác KHA cân tại K

c)BK cắt AH tại G. Chứng minh G là trọng tâm tam giác ABC và tính độ dài AG biết AB = 13cm, BC = 10cm

#Toán lớp 7

linhtieuthu

17 tháng 4 2016 - olm

cho tam giác ABC cân tại A có AD là đường phân giác . Gọi G là trọng tâm của tam giác ABC . Tính GD biết AB=13cm, BC=10cm.

#Toán lớp 7

Devil

17 tháng 4 2016

xét tam giác ABD và tam giác ACD có:

AB=AC

AD(chung)

BAD=CAD(gt)

suy ra tam giác ABD=ACD(c.g.c)

suy ra _ADB=ADC mà ADC+ADB=180 suy ra ADC=ADB=180/2=90

-DB=DC=1/2BC=5cm

vì AD là 1 đường trung tuyến của tam giác ABC, G là trọng tâm của tam giác ABC suy ra GD=1/3AD

ta có:\(AD^2=AB^2-BD^2=13^2-5^2=169-25=144\)

\(AD=\sqrt{144}=12\left(cm\right)\)

GD=1/3AD=1/3x12=4(cm)

Đúng(1)

Nhi Vũ

8 tháng 5 2022

Tam giác ABC cân tại A có AB=5cm; BC=8cm. Gọi G là trọng tâm của tam giác đó thì độ dài của AG sẽ là bao nhiêu?

A. AG = 1cm

B. AG = 2cm

C. AG = 3cm

D. AG = 4cm

giúp mình với ạ

#Toán lớp 7

Đinh Minh Đức

8 tháng 5 2022

đề bài bị lỗi (mik nghĩ vậy)

Đúng(0)

Khanh Pham

8 tháng 5 2022

Đúng(2)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP