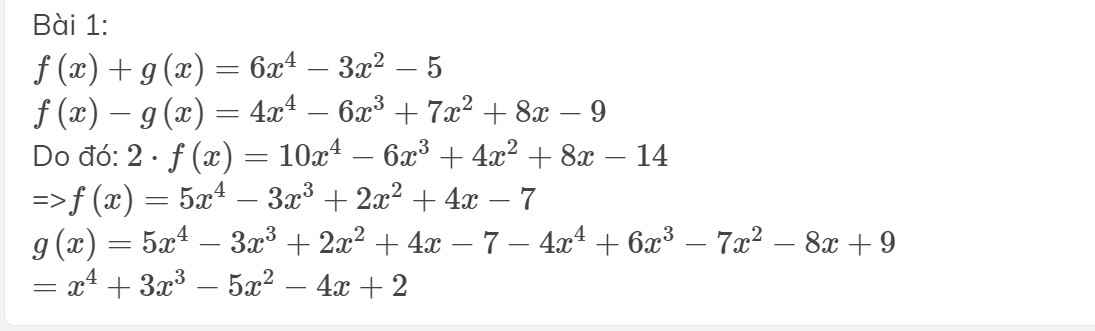Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Bài 1:
\(f\left(x\right)+g\left(x\right)=6x^4-3x^2-5\)
\(f\left(x\right)-g\left(x\right)=4x^4-6x^3+7x^2+8x-9\)
Do đó: \(2\cdot f\left(x\right)=10x^4-6x^3+4x^2+8x-14\)
=>\(f\left(x\right)=5x^4-3x^3+2x^2+4x-7\)
\(g\left(x\right)=5x^4-3x^3+2x^2+4x-7-4x^4+6x^3-7x^2-8x+9\)
\(=x^4+3x^3-5x^2-4x+2\)

Câu a, Gợi ý thôi nhé
\(f\left(x\right)=\frac{\left(f\left(x\right)+g\left(x\right)\right)+\left(f\left(x\right)-g\left(x\right)\right)}{2}\)
và \(g\left(x\right)=\frac{\left(f\left(x\right)+g\left(x\right)\right)-\left(f\left(x\right)-g\left(x\right)\right)}{2}\)
thay biểu thức trên vào là ra nhé
b, Chú ý: f(100) sẽ có x-100=0 nhé, nên em tách các số ra sao cho có chứa x-100 để nó bằng 0 nhé
ví dụ: \(x^8-100x^7=x^7\left(x-100\right)\), các chỗ khác tách tương tự, đề này em gõ anh nghĩ bị sai đề ròi nhé

Bài 2:
x=100 nên x+1=101
\(f\left(x\right)=x^8-x^7\left(x+1\right)+x^6\left(x+1\right)-x^5\left(x+1\right)\)
\(=x^8-x^8-x^7+x^7+x^6-x^6-x^5\)
\(=-x^5=-100^5\)