Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Xét (O) có
MA,MB là các tiếp tuyến
nên MA=MB
mà OA=OB
nên OM là đường trung trực của AB
=>OM vuông góc với AB
Ta có: ΔOAB cân tại O
mà OK là đường cao
nên K là trug điểm của BA
=>AB=2AK
Xét tứ giác OAMB có góc OAM+góc OBM=180 độ
nên OAMB là tứ giác nội tiếp(1)
Xét tứ giác OAMH có góc OAM+góc OHM=180 độ
nên OAMH là tứ giác nội tiếp(2)
Từ (1) và (2) suy ra O,A,M,B,H cùng thuộc 1 đường tròn
2: Xét ΔOBI và ΔOHB có
góc OBI=góc OHB
góc IOB chung
DO đó: ΔOBI đồng dạng với ΔOHB
=>OB/OH=OI/OB
=>OI*OH=OB^2=R^2
Xét ΔOAM vuông tại A có AK là đường cao
nên OK*OM=OA^2=R^2

a: OH*OM=OA^2=R^2
b: ΔOCD cân tại O
mà OI là đường trung tuyến
nên OI vuông góc với CD
Xét tứ giác OIAM có
góc OIM=góc OAM=90 độ
nên OIAM là tứ giác nội tiếp
c: Xét ΔOHK vuông tại H và ΔOIM vuông tại I có
góc HOK chung
Do đo: ΔOHK đồng dạng với ΔOIM
=>OH/OI=OK/OM
=>OI*OK=OH*OM=R^2=OC^2
mà CI vuông góc với OK
nên ΔOCK vuông tại C
=>KC là tiếp tuyến của (O)

1) Ta có : OA=OB=R; MA=MB(t/chất tiếp tuyến)
=>OM là trung trực của AB.Nên AB=2AK
Gọi G là trung điểm OM theo tính chất đường trung tuyến tam giác vuông ta có OG=GA=GB=GM=GH => M,A,O,B,H cùng thuộc một đường tròn.
2) Tam giác OKI đồng dạng với tam giác OHM (g-g)
=>\(\dfrac{OI}{OM}=\dfrac{OK}{OH}\) =>OI.OH=OK.OM=BK.BK=R.R
Câu 3 làm như thế nào vậy
Mình cx có cùng câu hỏi với bạn linh

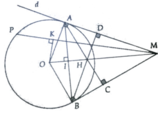
a, HS tự làm
b, Chú ý O K M ^ = 90 0 và kết hợp ý a) => A,M,B,O,K ∈ đường tròn đường kính OM
c, Sử dụng hệ thức lượng trong tam giác vuông OAM ( hoặc có thể chứng minh tam giác đồng dạng)
d, Chứng minh OAHB là hình bình hành và chú ý A,B thuộc (O;R) suy ra OAHB là hình thoi
e, Chứng minh OH ⊥ AB, OMAB => O,H,M thẳng hàng


