Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bạn ơi cho mình hỏi bài này ở đề năm bao nhiêu của thành phố nào vậy bạn?????
3. Xét tứ giác BFHD có:
HFB + HDB = 90º + 90º = 180º => BFHD là tứ giác nội tiếp. ⇒ FBH = FDH (1)
Tương tự có DHEC là tứ giác nội tiếp, ⇒HCE = HDE (2)
Mà BFEC là tứ giác nội tiếp nên FCE = FBE (3)
Từ (1) (2) (3)⇒ 2ABE = FDH + HDE = FDE
Vì BFEC là tứ giác nội tiếp đường tròn tâm I, đường kính BC nên theo quan hệ giữa góc ở tâm và góc nội tiếp cùng chắn cung EF, ta có: FIE = 2.FBE = 2.ABE
⇒FIE = FDE
4.Vì BFEC là tứ giác nội tiếp nên:
ABC = 180º – FEC = AEF => ΔAEF ~ ΔABC (g.g)![]()
Suy ra độ dài EF không đổi khi A chạy trên cung lớn BC của đường tròn (O)
Gọi K là giao điểm thứ 2 của ED và đường tròn đường kính BC
Theo tính chất góc ngoài: FDE = DKE + DEK
Theo ý 3 và quan hệ giữa góc ở tâm và góc nội tiếp cùng chắn cung, có FDE = FIE = 2.DKE
⇒DKE = DEK => ΔDEK cân tại D => DE = DK
Chu vi ΔDEF là P = DE + EF + FD = EF + FD + DK = EF + FK
Có FK ≤ BC ( dây cung – đường kính) => P ≤ EF + BC không đổi
Dâu bằng xảy ra khi và chỉ khi FK đi qua I ⇔ D trùng I ⇔ ΔABC cân tại A.
Vậy A là điểm chính giữa của cung lớn BC

B C A H E Q F P D
a/
Ta thấy F và E đều nhìn BC dưới cùng 1 góc 90 độ nên E,F nằm trên đường tròn đường kính BC ta gọi là đường tròn (O')
=> B,F,E,C cùng nawmg trên một đường tròn
b/
Xét đường tròn (O) ta có
sđ \(\widehat{BQP}=\) sđ \(\widehat{BCP}=\frac{1}{2}\) sđ cung BP (góc nội tiếp đường tròn) (1)
Xét đường tròn (O') ta có
sđ \(\widehat{BEF}=\) sđ \(\widehat{BCP}=\frac{1}{2}\) sđ cung BF (góc nội tiếp đường tròn) (2)
Từ (1) và (2) \(\Rightarrow\widehat{BQP}=\widehat{BEF}\) => PQ//EF (Hai đường thẳng bị cắt bởi đường thẳng thứ 3 có hai góc ở vị trí đồng vị thì chúng // với nhau
c/ ta thấy F và D cùng nhìn BH dưới cùng 1 góc 90 độ nên BDHF là tứ giác nội tiếp
sđ \(\widehat{ABE}=\)sđ \(\widehat{FDA}=\frac{1}{2}\) sđ cung FH (1)
Ta thấy D và E cùng nhìn AB đướ cùng 1 góc 90 độ nên ABDE là tứ giác nội tiếp
sđ \(\widehat{ABE}=\)sđ \(\widehat{ADE}=\frac{1}{2}\) sđ cung AE (2)
Mà \(\widehat{FDA}+\widehat{ADE}=\widehat{FDE}\) (3)
Từ (1) (2) và (3) \(\Rightarrow\widehat{FDE}=2.\widehat{ABE}\left(dpcm\right)\)

1) Xét tứ giác BCEF có
\(\widehat{BEC}=\widehat{BFC}\left(=90^0\right)\)
mà hai góc này cùng nhìn cạnh BC dưới những góc bằng nhau
nên BCEF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
2) Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{FAC}\) chung
Do đó: ΔAEB\(\sim\)ΔAFC(g-g)
Suy ra: \(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AE\cdot AC=AF\cdot AB\)(Đpcm)

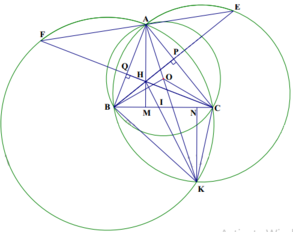
Gọi (O’) là đường tròn đi qua bốn điểm B, H,C, K. Ta có dây cung B C = R 3
BKC=60o= BAC nên bán kính đường tròn (O’) bằng bán kính R của đường tròn (O).
Gọi M là giao điểm của AH và BC thì MH vuông góc với BC, kẻ KN vuông góc với BC (N thuộc BC), gọi I là giao điểm của HK và BC.
Bài giảng học thử
Video không hỗ trỡ trên thiết bị của bạn!
Bài 8. Bài toán hai tiếp tuyến cắt nhau - Phần 2 - Tổng ôn Toán vào 10 - Cô Nguyễn Hồng Nhung
Video không hỗ trỡ trên thiết bị của bạn!
Bài 1. Đại cương về hệ phương trình bậc nhất 2 ẩn - Phần 3 - Tổng ôn Toán vào 10 - Cô Nguyễn Hồng Nhung
Video không hỗ trỡ trên thiết bị của bạn!
Bài 6. Ôn tập chương Phần 3 - Toán 9 - Thầy Trần Trung Hải
Video không hỗ trỡ trên thiết bị của bạn!
Dạng 1: Toán chuyển động - Phần 3. Chuyển động ngược xuôi trên sông - TỔNG ÔN Toán 9 - Cô Vương Thị Hạnh
Video không hỗ trỡ trên thiết bị của bạn!
Bài học 2: Đề số 3 (Phần 2) - LUYỆN ĐỀ ôn thi vào 10 - Cô Vương Thị Hạnh

A B C K D E F O I M
Ta giải như sau :
a) 1. Góc ACF + Góc BAC = 90 độ ; Góc EBA + BAC = 90 độ => Góc ACF = Góc EBA (cùng phu với Góc BAC)
Mà ACF và EBA là hai góc chắn cung EF của tứ giác EFBC và bằng nhau
=> Tứ giác EFBC nội tiếp.
2. Ta có : BE vuông góc với AC tại E ; CK vuông góc với AC tại C (Vì góc ACK chắn nửa cung tròn đường kính AK)
=> BE // CK (1)
Tương tự ta cũng có : BK // CF (2)
Từ (1) và (2) suy ra tứ giác BHCK là hình bình hành (dhnb)
b) Vì tứ giác BHCK là hình bình hành nên hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Mà M là trung điểm của BC => M cũng là trung điểm HK
Xét tam giác AHK có AM và HO lần lượt là hai đường trung tuyến ( AO = OK ; HM = MK) cắt nhau tại I
=> I là trọng tâm tam giác AHK
Lại có AM là đường trung tuyến tam giác ABC và I thuộc AM => I là trọng tâm tam giác ABC
c) Mình chưa nghĩ ra :))
giải như sau :
a) 1. Góc ACF + Góc BAC = 90 độ ; Góc EBA + BAC = 90 độ => Góc ACF = Góc EBA (cùng phu với Góc BAC)
Mà ACF và EBA là hai góc chắn cung EF của tứ giác EFBC và bằng nhau
=> Tứ giác EFBC nội tiếp.
2. Ta có : BE vuông góc với AC tại E ; CK vuông góc với AC tại C (Vì góc ACK chắn nửa cung tròn đường kính AK)
=> BE // CK (1)
Tương tự ta cũng có : BK // CF (2)
Từ (1) và (2) suy ra tứ giác BHCK là hình bình hành (dhnb)
b) Vì tứ giác BHCK là hình bình hành nên hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Mà M là trung điểm của BC => M cũng là trung điểm HK
Xét tam giác AHK có AM và HO lần lượt là hai đường trung tuyến ( AO = OK ; HM = MK) cắt nhau tại I
=> I là trọng tâm tam giác AHK
Lại có AM là đường trung tuyến tam giác ABC và I thuộc AM => I là trọng tâm tam giác ABC

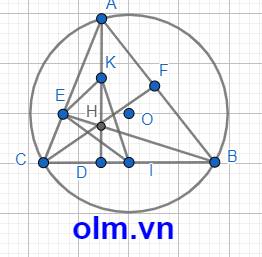
a, Xét tam giác vuông EBC vuông tại E và CI = IB
⇒ IE = IC = IB (1) ( vì trong tam giác vuông trung tuyến ứng với cạnh huyền bằng \(\dfrac{1}{2}\) cạnh huyền)
Xét tam giác vuông BCF vuông tại F và IC =IB
⇒IF = IC = IB (2) (vì trong tam giác vuông trung tuyến ứng với cạnh huyền bằng \(\dfrac{1}{2}\) cạnh huyền)
Từ (1) và (2) ta có:
IE = IF = IB = IC
Vậy bốn điểm B, C, E, F cùng thuộc một đường tròn tâm I bán kính bằng \(\dfrac{1}{2}\) BC (đpcm)
b, Xét \(\Delta\)AFC và \(\Delta\)AEB có:
\(\widehat{CAF}\) chung ; \(\widehat{AFC}\) = \(\widehat{AEB}\) = 900
⇒ \(\Delta\)AFC \(\sim\) \(\Delta\)AEB (g-g)
⇒ \(\dfrac{AF}{AE}\) = \(\dfrac{AC}{AB}\) (theo định nghĩa hai tam giác đồng dạng)
⇒AB.AF = AC.AE (đpcm)
Xét tam giác vuông AEH vuông tại E và KA = KH
⇒ KE = KH ( vì trong tam giác vuông trung tuyến ứng với cạnh huyền bằng \(\dfrac{1}{2}\) cạnh huyền)
⇒\(\Delta\)EKH cân tại K ⇒ \(\widehat{KEH}\) = \(\widehat{EHK}\)
\(\widehat{EHK}\) = \(\widehat{DHB}\) (vì hai góc đối đỉnh)
⇒ \(\widehat{KEH}\) = \(\widehat{DHB}\) ( tc bắc cầu) (3)
Theo (1) ta có: IE = IB ⇒ \(\Delta\) IEB cân tại I
⇒ \(\widehat{IEB}\) = \(\widehat{IBE}\) (4)
Cộng vế với vế của (3) và(4)
Ta có: \(\widehat{KEI}\) = \(\widehat{KEH}\) + \(\widehat{IEB}\) = \(\widehat{DHB}\) + \(\widehat{IBE}\) = \(\widehat{DHB}\) + \(\widehat{DBH}\)
Vì tam giác DHB vuông tại D nên \(\widehat{DHB}\) + \(\widehat{DBH}\) = 1800 - 900 = 900
⇒\(\widehat{KEI}\) = 900
IE \(\perp\) KE (đpcm)