Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

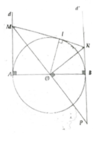
a, ∆MAO = ∆PBO => MO = OP => ∆MNP cân
Vì đường cao NO đồng thời là đường trung tuyến
b, 1 O I 2 - 1 O M 2 + 1 O N 2
= 1 O P 2 + 1 O N 2 = 1 O B 2 => OI = R
=> MN là tiếp tuyến của (O)
c, AM.BN = MI.IN = O I 2 = R 2
d, S A M N B = M N . A B 2
=> S A M N B min
<=> M N m i n <=> AM = R

O B A M D N I
a) Ta thấy ngay \(\Delta MAO=\Delta DBO\) (Cạnh góc vuông và góc nhọn kề)
\(\Rightarrow MO=DO\)
Xét tam giác MNP có NO là đường cao đồng thời trung tuyến nên tam giác MNP cân tại N.
b) Do tam giác MNP cân tại N nên NO cũng đồng thời là phân giác.
Vậy thì \(\Delta ION=\Delta BON\) (Cạnh huyền góc nhọn)
\(\Rightarrow OI=OB=R\)
Lại có \(OI\perp MN\Rightarrow\) MN vuông góc OI tại I hay MN là tiếp tuyến của (O)
c) Ta thấy ngay \(AM.BN=MI.IN\)
Xét tam giác vuông MON có OI là đường cao nên \(MI.IN=OI^2=R^2\)
\(\Rightarrow AM.BN=R^2\)
d) Do AM và BN cùng vuông góc với AB nên ANNB là hình thang vuông
\(S_{AMNB}=\frac{\left(AM+NB\right).AB}{2}=\frac{\left(MI+IN\right).AB}{2}=\frac{MN.AB}{2}\)
Do AB không đổi nên diện tích hình thang vuông AMNB nhỏ nhất khi MN nhỏ nhất.
MN là đường xiên nên nó nhỏ nhất khi là đường vuông góc, nói cách khác là tứ giác AMNB là hình chữ nhật.
Khi đó AM = OI = R.
Vậy khi M cách O một khoảng bằng R thì diện tích tứ giác AMNB nhỏ nhất.
a: Xét ΔOAM vuông tại A vầ ΔOBP vuông tại B có
OA=OB
góc AOM=góc BOP
Do đó: ΔOAM=ΔOBP
=>OM=OP
Xét ΔNMP có
NO vừa là đường cao, vừa là trung tuyến
nên ΔNMP cân tại N
b: góc NMO=góc NPO
=>góc NMO=góc AMO
Xét ΔMAO và ΔMIO có
MO chung
góc AMO=góc IMO
Do đo: ΔMAO=ΔMIO
=>OI=OA=R
=>MN là tiếp tuyến của (O)