Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x C A O B K y D
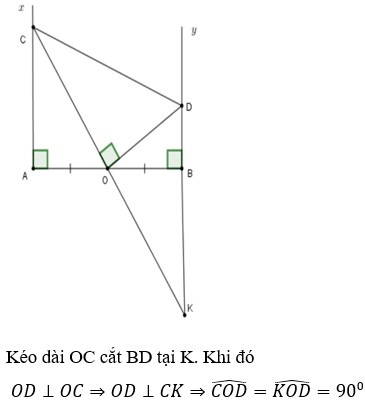
Gọi K là giao điểm của CO và BD
Xét \(\Delta\)AOC và \(\Delta\)BOK có :
AO = BO(gt)
\(\widehat{OAC}=\widehat{OBK}\left(=90^0\right)\)
\(\widehat{O}\)chung
=> \(\Delta\)AOC = \(\Delta\)BOK(g.c.g)
=> OC = OK(hai cạnh tương ứng)
AC = BK(hai cạnh tương ứng)
Xét \(\Delta\)COD và \(\Delta\)KOD có :
CO = KO(gt)
\(\widehat{OCD}=\widehat{OKD}\left(=90^0\right)\)
OD cạnh chung
=> \(\Delta\)COD = \(\Delta\)KOD(c.g.c)
=> CD = KD(hai cạnh tương ứng)
Do đó : CD = DB + BK = DB + AC

Ta có hình vẽ:
d N M A B C
Ta có:
góc MAB = góc ABC mà MAB và ABC ở vị trí so le trong => AM // BC (1)
góc NAC = góc ACB mà NAC và ACB ở vị trí so le trong => AN // BC (2)
Từ (1) và (2) mà theo tiên đề Ơ-clit qua 1 điểm nằm ngoài 1 đường thẳng chỉ kẻ được đúng 1 đường thẳng song song với đường thẳng ban đầu => MA trùng với NA hay 3 điểm A, M, N thẳng hàng
=> MN // BC
Mà d vuông góc với BC, MN // BC => MN vuông góc với d (quan hệ từ vuông góc -> song song) (2)
Mặt khác, AM = AB, AB = AC, AC = AN
=> AM = AN hay A là trung điểm của MN (3)
Từ (2) và (3) => d là đường trung trực của MN (đpcm)

nguyễn xuân hoạt nếu biết thì hãy trả lời đừng trả lời kiểu đó nhé :))

a) Ta có MN vuông góc với AB ( do MN là đường trung trực của đoạn thẳng AB theo giả thuyết nên suy ra)
và đường thẳng m cũng vuông góc với đoạn thẳng AB ( theo giả thiết)
nên từ đó ta suy ra MN//m (đpcm)
b) Từ MN//m ta suy ra MIC=ICB (hai góc so le trong)
mà ICB= 60 độ => MIC=60 độ
c) Ta có HIB= HIN+NIB
Mặt khác HIN=MIC=60 độ ( so le trong)
và NIB=90 độ (gt)
suy ra HIB= 60+90=150 độ
d) Vì theo giả thiết ta có đường thẳng a đi qua C và song song với MN và điểm C lại nằm trên cùng một đường thẳng m với điểm B mà đường thẳng m lại song song với đường thẳng MN nên suy ra đường thẳng a trùng với đường thẳng m và đi qua B