Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc ONM+góc OPM=180 độ
=>ONMP nội tiếp
b: ONMP nội tiếp
=>góc NMO=góc NPO
c: Xét ΔMNA và ΔMBN có
góc MNA=góc MBN
góc NMA chung
=>ΔMNA đồng dạng với ΔMBN
=>MN/MB=MA/MN
=>MN^2=MB*MA

a: góc MNO+góc MPO=90+90=180 độ
=>MNOP nội tiếp
b: MNOP nội tiếp
=>góc NMO=góc NPO

a) zì H là trung điểm của AB nên \(OH\perp AB\)hay \(\widehat{OHM}=90^0\)
theo tính chất của tiếp tuyến ta lại có \(OD\perp DM\left(hay\right)\widehat{ODM}=90^0\)
=> M,D,O,H cùng nằm trên 1đường tròn
b) Theo tính chất tiếp tuyến ta có
MC=MD=> tam giác MDC cân tại M
=> MI là 1 đương phân giác của CMD , MẶt khác I là điểm chính giữa cung nhỏ CD nên :
\(\widehat{DCI}=\frac{1}{2}sđ\widebat{DI}=\frac{1}{2}sđ\widebat{CI}=\widehat{MCI}\)
=> CI là phân giác của góc MCD .
zậy I là tâm đường tròn nội tiếp tam giác MCD

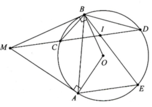
a, Vì M B C ^ = M D B ^ = 1 2 s đ C B ⏜ nên chứng minh được ∆MBC:∆MDB (g.g)
b, Vì
M
B
O
^
+
M
A
O
^
=
180
0
nên tứ giác MAOB nội tiếp
c, Đường tròn đường kính OM là đường tròn ngoại tiếp tứ giác MAOB => r = M O 2
Gọi H là giao điểm của AB với OM
=> OH ⊥ AB; AH = BH = R 3 2
Giải tam giác vuông OAM, đường cao AH ta được OM = 2R Þ r = R
d, Ta có M I B ^ = s đ D E ⏜ + s đ B C ⏜ 2 và M A B ^ = s đ A C ⏜ + s đ B C ⏜ 2
Vì AE song song CD => s đ D E ⏜ = s đ A C ⏜ => M I B ^ = M A B ^
Do tứ giác MAIB nội tiếp hay 5 điểm A, B, O, I, M nằm trên cùng 1 đường tròn kính MO
Từ đó ta có được M I O ^ = 90 0 => OI ⊥ CD hay I là trung điểm của CD

a) Tứ giác MAOB có: \(\widehat{OAM}=90^0\left(0A\perp AM\right);\widehat{OBM}=90^0\left(CB\perp BM\right)\)
=> \(\widehat{OAM}+\widehat{OBM}=180^O\)
=> AOBM nội tiếp (tổng 2 góc đối = 180)
Vì I là tâm=> I là trung điểm OM
b) Tính \(MA^2=3R^2\Rightarrow MC.MD=3R^2\)
c) CM: OM là trung trực AB
=> FA=FB
=> tam giác FAB cân tại F
Gọi H là giao điểm AB và OM
Ta có: OA=OB=AI=R => tam giác OAI đều
=> OAI =60O=> FAB=60o (cùng phụ AFI)
Vậy tam giác AFB đều
d) Kẻ EK vuông góc với FB tại K. Ta có:
\(S_{B\text{EF}}=\frac{1}{2}.FB.EK\)
Mà \(EK\le BE\)( TAM giác BEK vuông tại K)
Lại có: \(BE\le OA\)(LIÊN hệ đường kính và dây cung)
=> \(S_{B\text{EF}}\le\frac{1}{2}.R\sqrt{3}.2R=R^2\sqrt{3}\)
GTLN của \(S_{B\text{EF}}=R^2\sqrt{3}\). kHI ĐÓ BE là đường kính (I)
Kẻ đường kính BG của (I). Vì B và (I) cố định nên BG cố
định . Khi đó vị trí cắt tuyến MCD để \(S_{B\text{EF}}\)đạt GTLN là C là giao điểm của FG với đường tron (O)
a.
Do MC, MD là các tiếp tuyến \(\Rightarrow\widehat{DMO}=\widehat{DNO}=90^0\)
\(\Rightarrow\)M và N cùng nhìn OD dưới 1 góc vuông nên DMON nội tiếp
b.
Xét hai tam giác MIA và NIM có:
\(\left\{{}\begin{matrix}\widehat{MIA}-chung\\\widehat{IMA}=\widehat{INM}\left(\text{cùng chắn MA}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta MIA\sim\Delta NIM\left(g.g\right)\)
\(\Rightarrow\dfrac{MI}{IN}=\dfrac{IA}{MI}\Rightarrow MI^2=IA.IN\)
c.
Theo t/c hai tiếp tuyến cắt nhau ta có \(DM=DN\)
Lại có \(OM=ON=R\)
\(\Rightarrow OD\) là trung trực MN
\(\Rightarrow OD\) vuông góc MN tại H
Xét hai tam giác OHM và OMD có:
\(\left\{{}\begin{matrix}\widehat{MOH}-chung\\\widehat{OHM}=\widehat{OMD}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta OHM\sim\Delta OMD\left(g.g\right)\)
\(\Rightarrow\dfrac{OH}{OM}=\dfrac{OM}{OD}\Rightarrow OM^2=OH.OD\)
\(\Rightarrow R^2=OH.\left(OH+HD\right)=3.\left(3+5\right)=24\)
\(\Rightarrow R=2\sqrt{6}\)
Chỉ cần giải câu C thôi cũng được ạ