Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, xét tam giác ABD và tam giác ACD có : AD chung
AB = AC do tam giác ABC cân tại A (gt)
góc BAD = góc CAD do AD là phân giác của góc BAC (gt)
=> tam giác ABD = tam giác ACD (c-g-c)
b, tam giác ABD = tam giác ACD (câu a)
=> BD = DC (đn) mà D nằm giữa B; C
=> D là trung điểm của BC (đn)
=> AD là trung tuyến
CF là trung tuyến
CF cắt AD tại G
=> G là trong tâm của tam giác ABC (đl)
c, Ta có : tam giác EDC có EH vừa là đường trung tuyến vừa là đường cao
\(\Rightarrow\)tam giác EDC cân tại E
D, Vì EH // AD \(\Rightarrow\)theo định lí Ta - lét ta có : \(\frac{DH}{HC}=\frac{AE}{EC}\)
Mà HC = HD \(\Rightarrow\)AE = EC \(\Rightarrow\)E là trung điểm AC
\(\Leftrightarrow\)BE là đường trung tuyến \(\Rightarrow\)Ba điểm B, G , E thẳng hàng

ABDC E
a) Vì AD phân giác BACˆBAC^ (gt)
=> ABAC=BDDCABAC=BDDC (t/c đường p/g ΔΔ )
=> ABAC+AB=BDBD+DCABAC+AB=BDBD+DC (t/c TLT)
=> 1212+20=BDBC1212+20=BDBC
=> 1232=BD281232=BD28
=> BD=12⋅2832=10,5BD=12⋅2832=10,5 cm
Ta có: BD+DC=BCBD+DC=BC (D ∈∈ BC)
=> DC=28−10,5=17,5DC=28−10,5=17,5 cm
Xét ΔΔ ABC có: DE // AB (gt)
=> DEAB=DCBCDEAB=DCBC (hệ qủa ĐL Ta-lét)
=> DE=AB⋅DCBC=12⋅17,528=7,5DE=AB⋅DCBC=12⋅17,528=7,5 cm

I A B C E H D L G F K
a) Do I đối xứng với D qua H nên HI = HD.
Xét tứ giác BDEI có HI = HD; HB = HE nên BDEI là hình bình hành.
Lại có \(\widehat{EDB}=90^o\) nên BDEI là hình chữ nhật.
b) Do BDEI là hình chữ nhật nên IE // BD và IE = BD.
Vậy thì ta cũng có ngay IE // DL và IE = DL
Suy ra tứ giác IDLE là hình bình hành (dấu hiệu nhận biết)
c) Xét tam giác EBL có ED là đường cao đồng thời trung tuyến. Vậy tam giác EBL cân tại E hay \(\widehat{EBL}=\widehat{ELB}\)
Do tam giác ABC cân tại A nên \(\widehat{EBL}=\widehat{ACB}\) , suy ra \(\widehat{ACB}=\widehat{ELB}\)
Chúng lại ở vị trí đồng vị nên EL // GC.
Theo câu b, IDLE là hình bình hành nên IE // DL và ID // EL , vậy thì ID // GC
Xét tứ giác IGCD có: IG // DC; ID // GC nên IGDC là hình bình hành.
d) Ta có EG // BC nên tam giác AEG cân tại A hay AE = AG
Xét tam giác vuông FEG có AE = AG nên \(\widehat{AEG}=\widehat{AGE}\Rightarrow\widehat{AFE}=\widehat{AEF}\Rightarrow AE=AF\)
Vậy thì A là trung điểm EF.
Theo đề bài thì DFKC là hình chữ nhật nên FK song song và bằng DC
Lại có IGCD là hình bình hành nên IG song song và bằng DC.
Vậy thì FK song song và bằng IG hay FKGI là hình bình hành.
Suy ra FG và IK cắt nhau tại trung điểm mỗi đường.
A là trung điểm FG nên A là trung điểm IK. Vậy I, A, K thẳng hàng.
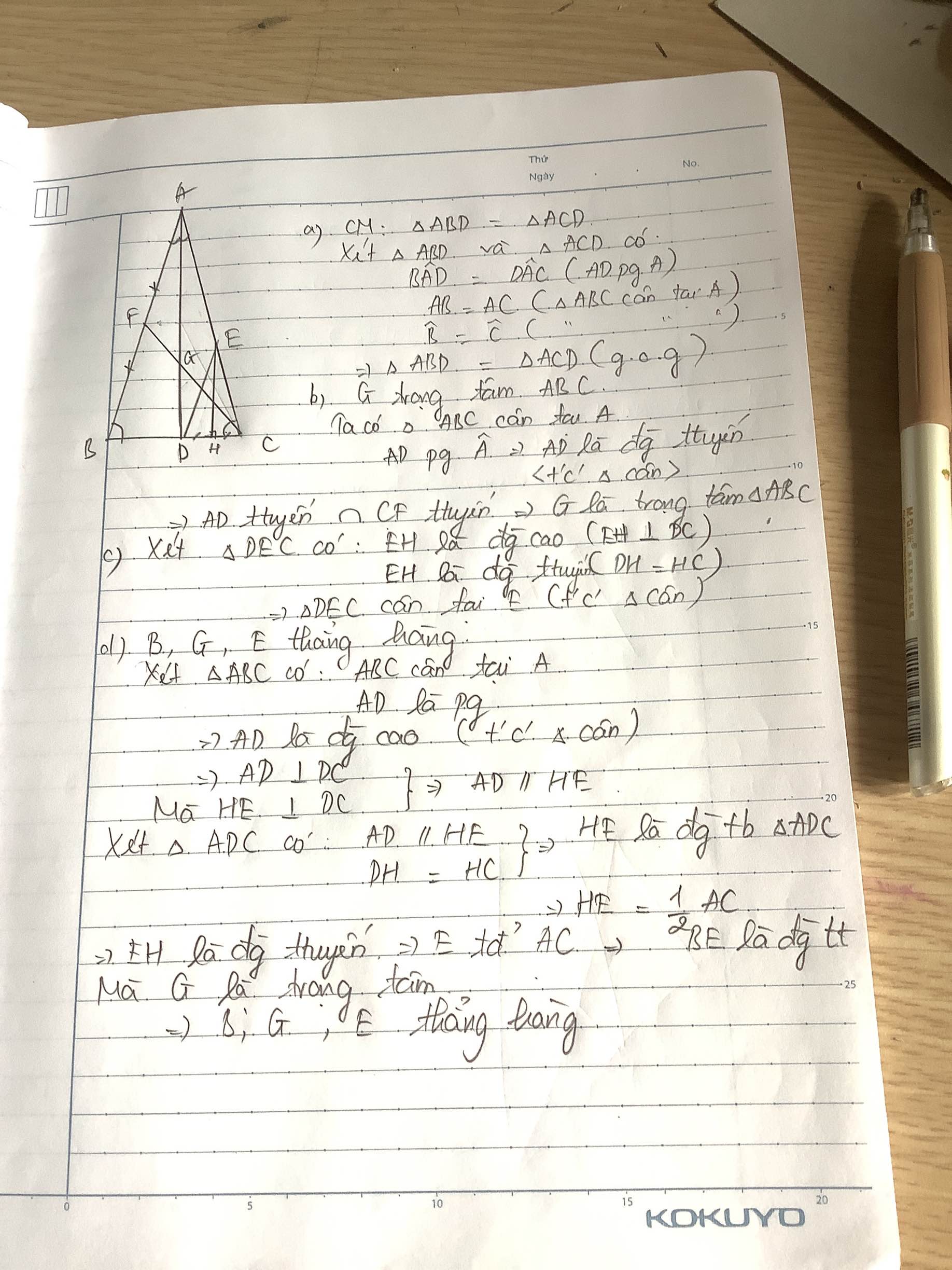


a) Xét ΔABD và ΔACD có:
AB = AC (gt)
BAD = CAD (gt)
cạnh AD chung
=> ΔABD = ΔACD (c.g.c) ( có thể CM theo g.c.g )
b) Vì ΔABD = ΔACD, ta có:
DC = DB ( hai cạnh tương ứng )
Mà tia AD cắt BC tại D ( D ∈ BC )
=> AD là đường trung tuyến ΔABC
=> G là trọng tâm ΔABC ( giao điểm hai đường trung tuyến )
c) Xét ΔEHC và ΔEHD có:
CH = DH (gt)
EHC = EHD ( = 90 o )
EH cạnh chung
=> ΔEHC = ΔEHD (c.g.c)
=> C = D
EC = ED
=> ΔDEC cân