Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Chú ý: Ab là phân giác góc D A M ^ ; AC là phân giác góc E A M ^ từ đó D A E ^ = 180 0
b, Sử dụng tính chất hai tiếp tuyến và hệ thức về đường cao và hình chiếu cạnh góc vuông lên cạnh huyền trong tam giác vuông BAC => BD.CE = BH.CH = C H 2 = D E 2 4
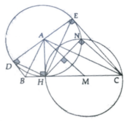
c, ∆HNC nội tiếp đường tròn (M) đường kính HC => HN ⊥ NC
Chứng minh AN là tiếp tuyến của (M)
Do đó AM ⊥ HN => AM//NC

A H B C M I D K F P Q G Note:Hình hơi lệch xíu ^^
a, Vì CM là tiếp tuyến của (A)
=> \(CM\perp AM\)
=> ^CMA = 90o
=> M thuộc đường tròn đường kính AC
Vì ^CHA = 90o
=> H thuộc đường tròn đường kính AC
Do đó : M và H cùng thuộc đường tròn đường kính AC
hay 4 điểm A,C,M,H cùng thuộc đường tròn đường kính AC
b, Vì AM = AH ( Bán kính)
CM = CH (tiếp tuyến)
=> AC là trung trực MH
=> \(AC\perp MH\)tại I
Xét \(\Delta\)AMC vuông tại M có MI là đường cao
\(\Rightarrow MA^2=AI.AC\)(Hệ thức lượng)
c, Vì CM , CH là tiếp tuyến của (A)
=> AC là phân giác ^HAM
=> ^HAC = ^MAC
Mà ^HAC + ^HAB = 90o
=> ^MAC + ^HAB = 90o
Ta có: ^BAD + ^BAC + ^CAM = 180o (Kề bù)
=> ^BAD + 90o + ^CAM = 180o
=> ^BAD + ^CAM = 90o
Do đó ^BAD = ^BAH (Cùng phụ ^CAM)
Xét \(\Delta\)BAD và \(\Delta\)BAH có:
AB chung
^BAD = ^BAH (cmt)
AD = AH (Bán kính (A) )
=> \(\Delta BAD=\Delta BAH\left(c.g.c\right)\)
=> ^ADB = ^AHB = 90o
\(\Rightarrow BD\perp AD\)
=> BD là tiếp tuyến của (A)
Làm đc đến đây thôi :(

A B C H D E I
a/ Xét \(\Delta ABC\) có
\(\widehat{ABC}+\widehat{ACB}=90^o\) (1)
Ta có
\(\widehat{ABD}=\widehat{ABC}\) (Hai tiếp tuyến cùng xp từ 1 điểm thì đường nối điểm đó với tâm đường tròn là phân giác của góc tạo bởi 2 tiếp tuyến) (2)
Ta có
\(\widehat{ACE}=\widehat{ACB}\) (Hai tiếp tuyến cùng xp từ 1 điểm thì đường nối điểm đó với tâm đường tròn là phân giác của góc tạo bởi 2 tiếp tuyến) (3)
Từ (1) (2) (3) \(\Rightarrow\widehat{ABD}+\widehat{ACE}=90^o\)
\(\Rightarrow\widehat{ABD}+\widehat{ACE}+\widehat{ABC}+\widehat{ACB}=180^o\)
\(\Rightarrow\left(\widehat{ABD}+\widehat{ABC}\right)+\left(\widehat{ACE}+\widehat{ACB}\right)=\widehat{DBC}+\widehat{ECB}=180^o\)
=> BD//CE (hai đường thẳng bị cắt bởi đường thẳng thứ 3 có hai góc trong cùng phía bù nhau thì chúng // với nhau)
Ta có
\(AD\perp BD\Rightarrow AD\perp CE\)
\(AE\perp CE\Rightarrow AE\perp BD\)
=> AD và AE cùng vuông góc với BD => AD và AE trùng nhau (Từ 1 điểm ở ngoài 1 đường thẳng chỉ dựng được duy nhất 1 đường thẳng vuông góc với đường thẳng đã cho) => D; A; E thẳng hàng
b/
Ta có \(\Delta ABC\) vuông tại A => A thuộc đường tròn đường kính BC. Gọi I là trung điểm BC nối AI ta có
BD//CE => BDEC là hình thang
AD=AE (bán kính (O))
IB=IC
=> AI là đường trung bình của hình thang BDEC => AI//CE mà \(CE\perp DE\Rightarrow AI\perp DE\) => DE là tiếp tuyến của đường tròn đường kính BC hay DE tiếp xúc với đường tròn đường kính BC
a) Theo tính chất của hai của hai tiếp tuyến cắt nhau, ta có:
^DAB=^BAH; ^HAC=^CAE.
Suy ra: ^DAE=^DAB+^BAH+^HAC+^CAE=2^BAH+2^HAC=2^BAC=180o.
Do ^DAE=180o nên DE là đường kính, suy ra D, E, A thẳng hàng.
b) Theo câu a: DE là đường kính đường tròn tâm A.
Có BD⊥DE,CE⊥DE. Suy ra BD//CE.
Gọi O là trung điểm BC.
Vậy tứ giác BDEC là hình thang. Do O và A lần lượt là trung điểm của BC, DE nên OA là đường trung bình của hình thang BDEC.
Suy ra OA⊥DE mà OA=BC2 nên OA là bán kính của đường tròn đường kính BC.
Thế thì DEDE tiếp xúc với đường tròn đường kính BCBC.

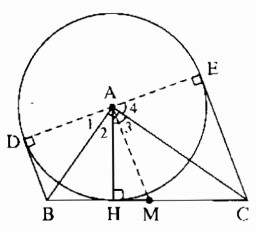
a) Theo tính chất hai tiếp tuyến cắt nhau ta có:
a) Theo tính chất hai tiếp tuyến cắt nhau ta có:
AB là tia phân giác của góc HAD
\(\Rightarrow\widehat{DAB}=\widehat{BAH}\)
AC là tia phân giác của góc HAE
\(\Rightarrow\widehat{HAD}=\widehat{CAE}\)
Ta có: \(\widehat{HAD}+\widehat{HEA}=2.\left(\widehat{BAH}+\widehat{HAC}\right)=2.\widehat{BAC}=2.90^o=180^o\)
Vậy ba điểm D, A, E thẳng hàng.
b) Gọi M là trung điểm của BC
Theo tính chất của tiếp tuyến, ta có: \(AD\downarrow BD;AE\downarrow CE\)
Suy ra: BD // CE
Vậy tứ giác BDEC là hình thang
Khi đó MA là đường trung bình của hình thang BDEC
Suy ra: \(MA\\ BD\Rightarrow MA\downarrow DE\)
Trong tam giác vuông ABC ta có: MA = MB = MC
Suy ra M là tâm đường tròn đường kính BC với MA là bán kính
Vậy DE là tiếp tuyến của đường tròn tâm M đường kính BC
a) theo tính chất 2 tiếp tuyến cắt nhau
ta có : DAB = BAH và HAC = CAE
DAH + HAE = 2(BAH + HAC) = 2.90 = 180
vậy D , A , E thẳng hàng

a: Xét (A;AH) có
AH là bán kính
BC\(\perp\)AH tại H
Do đó: BC là tiếp tuyến của (A;AH)
b: Xét (A) có
BH,BD là các tiếp tuyến
Do đó: BH=BD và AB là phân giác của góc HAD
Xét (A) có
CE,CH là các tiếp tuyến
Do đó: CE=CH và AC là phân giác của góc HAE
c: BD+CE
=BH+CH
=BC
d: AB là phân giác của góc HAD
=>\(\widehat{HAD}=2\cdot\widehat{HAB}\)
AC là phân giác của góc HAE
=>\(\widehat{HAE}=2\cdot\widehat{HAC}\)
Ta có: \(\widehat{HAD}+\widehat{HAE}=\widehat{EAD}\)
=>\(\widehat{EAD}=2\cdot\left(\widehat{HAB}+\widehat{HAC}\right)\)
=>\(\widehat{EAD}=2\cdot\widehat{BAC}=180^0\)
=>E,A,D thẳng hàng

a: Xét (A) có
BD,BH là các tiếp tuyến
nên BD=BH và AB là phân giác của góc HAD(1)
Xét (A) có
CH,CE là các tiếp tuyến
nên CH=CE và AC là phân giác của góc HAE(2)
BH+CH=BC
=>BC=CE+BD
b: Từ (1), (2) suy ra góc DAE=2*90=180 độ
=>D,A,E thẳng hàng
c: Gọi M là trung điểm của BC
Xét hình thang BDEC có
M,A lần lượt là trung điểm của BC,DE
nên MA là đường trung bình
=>MA//CE//BD
=>MA vuông góc với BC
=>DE là tiếp tuyến của (M)

a: Xét (A) có
BH,BD là các tiếp tuyến
Do đó: BH=BD và AB là phân giác của góc HAD
AB là phân giác của góc HAD
=>\(\widehat{HAD}=2\cdot\widehat{HAB}\)
Xét (A) có
CE,CH là các tiếp tuyến
Do đó: CE=CH và AC là phân giác của góc HAE
AC là phân giác của góc HAE
=>\(\widehat{HAE}=2\cdot\widehat{HAC}\)
Ta có: \(\widehat{HAE}+\widehat{HAD}=\widehat{DAE}\)
=>\(\widehat{DAE}=2\cdot\left(\widehat{HAB}+\widehat{HAC}\right)\)
=>\(\widehat{DAE}=2\cdot\widehat{BAC}=180^0\)
=>D,A,E thẳng hàng
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot HC=AH^2\)
=>\(BD\cdot CE=\left(\dfrac{1}{2}DE\right)^2=\dfrac{1}{4}DE^2\)
a) Ta có: \(\widehat{BAH}+\widehat{CAH}=\widehat{BAC}\)(tia AH nằm giữa hai tia AB,AC)
nên \(\widehat{BAH}+\widehat{CAH}=90^0\)
Xét (A) có
CE là tiếp tuyến có E là tiếp điểm(gt)
CH là tiếp tuyến có H là tiếp điểm(AH⊥CH tại H)
Do đó: AC là tia phân giác của \(\widehat{EAH}\)(Tính chất hai tiếp tuyến cắt nhau)
⇒\(\widehat{EAH}=2\cdot\widehat{HAC}\)
Xét (A) có
BH là tiếp tuyến có H là tiếp điểm(BH⊥AH tại H)
BD là tiếp tuyến có D là tiếp điểm(gt)
Do đó: AB là tia phân giác của \(\widehat{HAD}\)(Tính chất hai tiếp tuyến cắt nhau)
⇒\(\widehat{DAH}=2\cdot\widehat{HAB}\)
Ta có: \(\widehat{EAD}=\widehat{EAH}+\widehat{DAH}\)(tia AH nằm giữa hai tia AE,AD)
mà \(\widehat{EAH}=2\cdot\widehat{HAC}\)(cmt)
và \(\widehat{DAH}=2\cdot\widehat{HAB}\)(cmt)
nên \(\widehat{EAD}=2\cdot\widehat{HAC}+2\cdot\widehat{HAB}\)
\(\Leftrightarrow\widehat{EAD}=2\cdot\left(\widehat{HAC}+\widehat{HAB}\right)\)
\(\Leftrightarrow\widehat{EAD}=2\cdot90^0=180^0\)
hay A,D,E thẳng hàng(đpcm)
b) Xét (A) có
CE là tiếp tuyến có E là tiếp điểm(gt)
CH là tiếp tuyến có H là tiếp điểm(AH⊥CH tại H)
Do đó: CE=CH(Tính chất hai tiếp tuyến cắt nhau)
Xét (A) có
BH là tiếp tuyến có H là tiếp điểm(BH⊥AH tại H)
BD là tiếp tuyến có D là tiếp điểm(gt)
Do đó: BH=BD(Tính chất hai tiếp tuyến cắt nhau)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HC\cdot HB\)
hay \(AH^2=BD\cdot CE\)(1)
Ta có: AH=AE(=R)
mà AH=AD(=R)
nên AE=AD
mà E,A,D thẳng hàng(cmt)
nên A là trung điểm của ED
\(\Leftrightarrow EA=\dfrac{ED}{2}\)
\(\Leftrightarrow AH=\dfrac{ED}{2}\)
hay \(AH^2=\dfrac{DE^2}{4}\)(2)
Từ (1) và (2) suy ra \(BD\cdot CE=\dfrac{DE^2}{4}\)(đpcm)
c) Xét (M) có
ΔCNH nội tiếp đường tròn(C,N,H∈(M))
CH là đường kính
Do đó: ΔCNH vuông tại N(Định lí)
⇒CN⊥NH(3)
Vì (M) cắt (A) tại N và H
nên MA là đường trung trực của NH(Vị trí tương đối của hai đường tròn)
hay MA⊥NH(4)
Từ (3) và (4) suy ra CN//AM(Định lí 1 từ vuông góc tới song song)