Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

GTNN = -10
cách làm
M = ...
= 2(a2+b2)+a2+b2+c2
= 2(a2+b2)+(a+b+c)2-2(ab+bc+ac) (1)
mà ab+bc+ac=5
=> (1) = 2(a2+b2)+(a+b+c)2-10
có a2 và b2 \(\ge\) 0
2 >0
(a+b+c)2 \(\ge\) 0
=> (1) \(\ge\) -10
=> M min = -10
hơi sơ sài nhỉ, ko hiểu thì hỏi, tôi chỉ cho

Tìm GTNH: P=x^2+xy+y^2-3x-3y+2010? - Yahoo Hỏi & Đáp
https://vn.answers.yahoo.com/question/index?qid=20100903224130AAhmqxW

1, Ta có: 3-x2+2x=-(x2-2x+1)+4=-(x-1)2+4
vì (x-1)2 luôn lớn hơn hoặc bằng không với mọi x-->-(x-1)2 nhỏ hơn hoặc bằng 0 với mọi x
vậy giá trị lớn nhất của biểu thức 3-x2+2x là 4
các bài giá trị nhỏ nhất còn lại làm tương tự bạn nhé
chỉ cần đưa về nhân tử chung hoặc hằng đẳng thức là được


cháu tôi học ghê thế :))
a) 3x3 - 7x2 + 17x - 5
= 3x3 - x2 - 6x2 + 2x + 15x - 5
= x2( 3x - 1 ) - 2x( 3x - 1 ) + 5( 3x - 1 )
= ( 3x - 1 )( x2 - 2x + 5 )
b) Đặt A = a2 + ab + b2 - 3a - 3b + 3
=> 4A = 4a2 + 4ab + 4b2 - 12a - 12b + 12
= ( 4a2 + 4ab + b2 - 12a - 6b + 9 ) + ( 3b2 - 6b + 3 )
= ( 2a + b - 3 )2 + 3( b - 1 )2 ≥ 0 ∀ a, b
hay 4A ≥ 0 => A ≥ 0
Dấu "=" xảy ra <=> a = b = 1
a.
\(3x^3-7x^2+17x-5=3x^3-x^2-6x^2+2x+15x-5\)
\(=\left(3x-1\right)\left[x^2-2x+5\right]\)
b.\(a^2+ab+b^2-3a-3b+3=\left(a-1\right)^2+\left(b-1\right)^2+\left(a-1\right)\left(b-1\right)\)
\(=\left[a-1+\frac{b-1}{2}\right]^2+\frac{3}{4}\left(b-1\right)^2\ge0\)
dấu bằng xảy ra khi \(a-1=b-1=0\Leftrightarrow a=b=1\)


a) \(A=4x^2-12x+100=\left(2x\right)^2-12x+3^2+91=\left(2x-3\right)^2+91\)
Ta có: \(\left(2x-3\right)^2\ge0\forall x\inℤ\)
\(\Rightarrow\left(2x-3\right)^2+91\ge91\)
hay A \(\ge91\)
Dấu "=" xảy ra <=> \(\left(2x-3\right)^2=0\)
<=> 2x-3=0
<=> 2x=3
<=> \(x=\frac{3}{2}\)
Vậy Min A=91 đạt được khi \(x=\frac{3}{2}\)
b) \(B=-x^2-x+1=-\left(x^2+x-1\right)=-\left(x^2+x+\frac{1}{4}-\frac{5}{4}\right)=-\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\)
Ta có: \(-\left(x+\frac{1}{2}\right)^2\le0\forall x\)
\(\Rightarrow-\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\le\frac{5}{4}\) hay B\(\le\frac{5}{4}\)
Dấu "=" \(\Leftrightarrow-\left(x+\frac{1}{2}\right)^2=0\)
\(\Leftrightarrow x+\frac{1}{2}=0\)
\(\Leftrightarrow x=\frac{-1}{2}\)
Vậy Max B=\(\frac{5}{4}\)đạt được khi \(x=\frac{-1}{2}\)
\(C=2x^2+2xy+y^2-2x+2y+2\)
\(C=x^2+2x\left(y-1\right)+\left(y-1\right)^2+x^2+1\)
\(\Leftrightarrow C=\left(x+y-1\right)^2+x^2+1\)
Ta có:
\(\hept{\begin{cases}\left(x+y-1\right)^2\ge0\forall x;y\inℤ\\x^2\ge0\forall x\inℤ\end{cases}}\)
\(\Leftrightarrow\left(x+y-1\right)^2+x^2+1\ge1\)
hay C\(\ge\)1
Dấu "=" xảy ra khi \(\hept{\begin{cases}\left(x+y-1\right)^2=0\\x^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x+y=1\\x=0\end{cases}\Leftrightarrow}\hept{\begin{cases}y=1\\x=0\end{cases}}}\)
Vậy Min C=1 đạt được khi y=1 và x=0
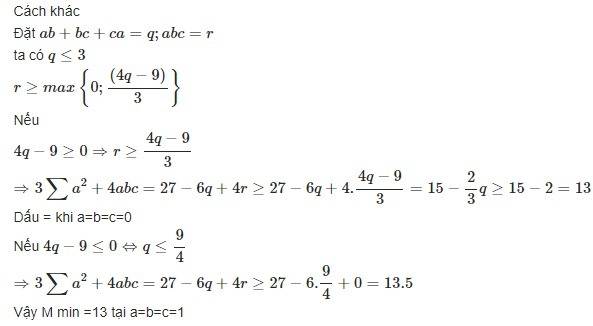
Với các bài toán tìm max, min 2 biến kiểu như thế này, em hay cố gắng nhân M lên n lần để tạo thêm được các số hạng, sang đó ghép tạo thành các bình phương.
Cách làm như sau:
\(4M=4a^2+4ab+4b^2-12a-12b+8004\)
\(=\left(4a^2+4ab+b^2\right)-6\left(2a+b\right)+3\left(b^2-2b\right)+8004\)
\(=\left(2a+b\right)^2-6\left(2a+b\right)+9+3\left(b^2-2b+1\right)+7992\)
\(=\left(2a+b-3\right)^2+3\left(b-1\right)^2+7992\ge7992\)
Vậy 4M min = 7992, vây M min = 1998.
Vậy min M = 1998 khi \(\hept{\begin{cases}b-1=0\\2a+b-3=0\end{cases}}\Rightarrow\hept{\begin{cases}b=1\\a=1\end{cases}}\)