Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\overrightarrow {GD} = - \overrightarrow {DG} \)
\( \Rightarrow \overrightarrow v = \overrightarrow {DE} + ( - \overrightarrow {DG} ) = \overrightarrow {DE} + \overrightarrow {GD} \)
\( \Rightarrow \overrightarrow v = \overrightarrow {GD} + \overrightarrow {DE} = \overrightarrow {GE} \) (tính chất giao hóan)
Chọn B.

1) Tự vẽ hình nha :3
Ta có:
\(\overrightarrow{NA}+\overrightarrow{NB}=2\overrightarrow{NM}\) (M là trung điểm AB)
Mà MN là đường trung bình của tam giác ABC \(\Rightarrow\overrightarrow{CB}=2\overrightarrow{NM}\)
\(\Rightarrow\overrightarrow{NA}+\overrightarrow{NB}=\overrightarrow{CB}\)
2) Khẳng định B đúng (điểm đầu điểm cuối của hai vecto giống nhau thì khi cộng lại sẽ mất đi)

Các kí hiệu bên dưới đều là vecto chứ ko phải đoạn thẳng:
a/ \(BB'+CC'+BA+CA=2AA'+BA+CA\)
\(=2\left(AB+BA'\right)+BA+CA=2AB+2BA'+BA+CA\)
\(=AB+CA+2BA'=CB+2BA'=CA'+A'B+2BA'\)
\(=BA'+CA'\)
b/ \(AA'+BB'+CC'=AB+BA'+BC+CB'+CA+AC'\)
\(=AB+BC+CA+BA'+CB'+AC'\)
\(=AC+CA+BA'+CB'+AC'\)
\(=BA'+CB'+AC'\)

a) Gọi M, N lần lượt là điểm đầu và điểm cuối của vecto \(\overrightarrow a \).
Vì \(\overrightarrow a = \overrightarrow {AB} \Leftrightarrow \overrightarrow {MN} = \overrightarrow {AB} \) nên tứ giác MNBA là hình bình hành.
Nói cách khác B là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow a \) và điểm A.
Tương tự, C là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow b \) và điểm B.
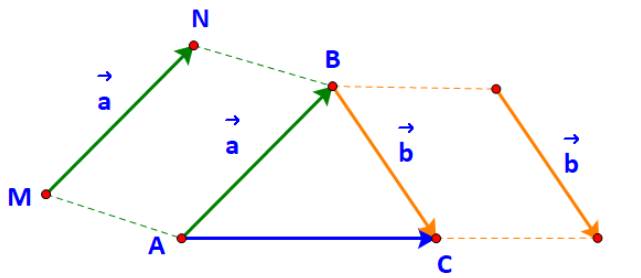
b) Dễ thấy: tổng của hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) là vecto \(\overrightarrow {AC} \).
Do đó tổng của hai vecto \(\overrightarrow a \) và \(\overrightarrow b \)bằng vecto \(\overrightarrow {AC} \).
Ta có viết: \(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Vận dụng tính chất giao hoán ta có: \[\overrightarrow u = \overrightarrow {NP} + \overrightarrow {MN} = \overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \]
Chọn C.