Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đường thẳng a chia mặt phẳng ra thành 2 nửa mặt phẳng bằng nhau.
Xét 3 trường hợp:
- Nếu cả 4 điểm A,B,C,D cùng nằm trên mặt nửa mặt phẳng bờ a thì đường thẳng a không cắt đoạn thẳng nào cả.
- Nếu có 1 điểm (Ví dụ là điểm A thuộc một nửa mặt phẳng) còn 3 điểm B,C,D thuộc nửa mặt phẳng đối thì đường thẳng a cắt 3 đoạn thẳng AB,AC,AD.
- Nếu có 2 điểm thuộc một nửa mặt phẳng (A,B) hai điểm kia (C,D) thuộc mooitj nửa mặt phẳng đối thì đường thẳng a cắt 4 đoạn thẳng AC,AD,BC,BD. =>đpcm.

Đáp án D
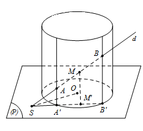
Gọi P là mặt phẳng đi qua S và vuông góc với trục của mặt T . Mặt phẳng P cắt T theo giao tuyến một đường tròn. Chiếu A, B, M theo phương vuông góc với mặt phẳng P ta được các điểm theo thứ tự là A ' , B ' , M ' thẳng hàng với S, trong đó A’,B’ nằm trên đường tròn tâm O trong mặt phẳng P và M’là trung điểm của A’B’. Do đó M’ luôn nằm trên đường tròn đường kính SO trong mặt phẳng P và MM’ vuông góc với P . Vậy MM’ nằm trên mặt trụ T ' chứa đường tròn đường kính SO và có trục song song với trục của mặt trụ T .

Đáp án B.
Các phương trình O x y : z = 0 ; O x y : x = 0 ; O x y : y = 0 . Giả sử M x M ; y M ; 0 , N x N ; 0 ; z N , P 0 ; y p ; z p . Tính theo giả thiết có M là trung điểm của AN nên ta có M 6 + x N 2 ; − 3 2 ; 4 + z N 2 . Do z M = 0 nên 4 + z N 2 = 0 ⇔ z N = − 4 ⇒ M x M ; − 3 2 ; 0 và N x N ; 0 ; − 4 .
Lại có N là trung điểm của MP nên N x M 2 ; 2 y P − 3 4 ; z P 2 .
Mà y N = 0 z N = − 4 nên 2 y P − 3 4 = 0 z P 2 = − 4 ⇔ y P = 3 2 z P = − 8 Khi đó P 0 ; 3 2 ; − 8 .
Từ
x M = 6 + x N 2 x M = x M 2 ⇔ 2 x M − x N = 6 x M − 2 x N = 0 ⇔ x M = 4 x N = 2
Vậy M 4 ; − 3 2 ; 0 , N 2 ; 0 ; − 4 .
Mặt khác
A B → = 2 A N → ⇔ x B − 6 = 2 ( 2 − 6 ) y B + 3 = 2 ( 0 + 3 ) z B − 4 = 2 ( − 4 − 4 ) ⇒ B ( − 2 ; 3 ; − 12 ) ⇒ a = − 2 b = 3 c = − 12 .
Vậy a + b + c = − 2 + 3 − 12 = − 11

4588
4558