Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Vì M ∈ O x y , M ∈ O x z , P ∈ O y z ⇒ z M = , y N = 0 , z P = 0
Mà M,N,P nằm trên đoạn AB sao cho A M = M N = N P = P B ⇒ A M ¯ = M N ¯ = N P ¯ = P B ¯
Khi đó A B ¯ = 4 A M ¯ ⇒ c - 5 = 4 z M - 5 ⇒ c = - 15 .
Lại có: A B ¯ = 2 A N ¯ ⇒ b + 3 = 2 y N + 3 ⇒ b = 3 .
A B ¯ = 4 P B ¯ ⇒ a - 9 = 4 a + x P ⇒ a = - 3 ⇒ a + b + c = - 15 .

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2

bài 1
\(A+B=a+b-5-b-c+1=a-c-4\)
\(A+B+C+D=a-c-4+b-c-4+b-a=2b-2c\)
\(A-B+C-D=a+b-5+b+c-1+b-c-4+a-b\)
\(A-B+C-D=2a+2b-10\)
\(A+B=a-c-4\)
\(C-D=b-c-4-b+a=a-c-4\)
\(A+B=C-D\)

ta có \(\left|x-a\right|+\left|x-b\right|+\left|x-c\right|+\left|x-d\right|\ge\left|\left(x-a\right)+\left(x-b\right)+\left(c-x\right)+\left(d-x\right)\right|=\left|c+d-a-b\right|=c+d-a-b\)( do a<b<c<d => c-a>0 và d-b>0)
vậy Min A= c+d-a-b

Làm thế nào nhiều gấp ba số nguyên (a, b, c) là có như vậy mà a.b.c√ = 6

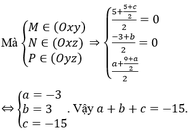
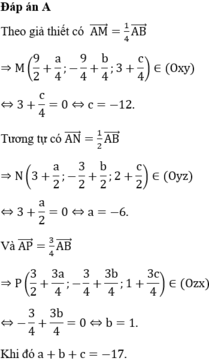


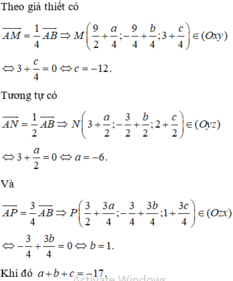
Đáp án B.
Các phương trình O x y : z = 0 ; O x y : x = 0 ; O x y : y = 0 . Giả sử M x M ; y M ; 0 , N x N ; 0 ; z N , P 0 ; y p ; z p . Tính theo giả thiết có M là trung điểm của AN nên ta có M 6 + x N 2 ; − 3 2 ; 4 + z N 2 . Do z M = 0 nên 4 + z N 2 = 0 ⇔ z N = − 4 ⇒ M x M ; − 3 2 ; 0 và N x N ; 0 ; − 4 .
Lại có N là trung điểm của MP nên N x M 2 ; 2 y P − 3 4 ; z P 2 .
Mà y N = 0 z N = − 4 nên 2 y P − 3 4 = 0 z P 2 = − 4 ⇔ y P = 3 2 z P = − 8 Khi đó P 0 ; 3 2 ; − 8 .
Từ
x M = 6 + x N 2 x M = x M 2 ⇔ 2 x M − x N = 6 x M − 2 x N = 0 ⇔ x M = 4 x N = 2
Vậy M 4 ; − 3 2 ; 0 , N 2 ; 0 ; − 4 .
Mặt khác
A B → = 2 A N → ⇔ x B − 6 = 2 ( 2 − 6 ) y B + 3 = 2 ( 0 + 3 ) z B − 4 = 2 ( − 4 − 4 ) ⇒ B ( − 2 ; 3 ; − 12 ) ⇒ a = − 2 b = 3 c = − 12 .
Vậy a + b + c = − 2 + 3 − 12 = − 11