K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

TP
14 tháng 4 2018
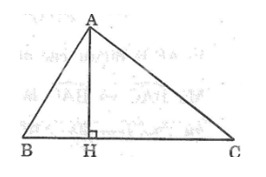
Trong ΔABC ta có ∠AC > ∠AB (gt)
Suy ra: ∠B > ∠C (đối diện cạnh lớn hơn là góc lớn hơn)
Trong ΔAHB có ∠(AHB) = 90o
Suy ra: ∠B + ∠(HAB) = 90o (tính chất tam giác vuông) (1)
Trong ΔAHC có ∠(AHC) = 90o
Suy ra: ∠C + ∠(HAC) = 90o (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: ∠B + ∠(HAB) = ∠C + ∠(HAC)
Mà ∠B > ∠C nên ∠(HAB) < ∠(HAC) .
Lời giải:
a. Trong tam giác $ABC$ có $AC> AB$, mà $\widehat{B}$ đối diện cạnh $AC$, $\widehat{C}$ đối diện $AB$ nên $\widehat{B}> \widehat{C}$
b. Có:
$\widehat{B}=90^0-\widehat{BAH}=\widehat{HAC}$
$\widehat{C}=90^0-\widehat{HAC}=\widehat{BAH}$
c.
Xét tam giác $ABH$ vuông tại $H$ có $AB$ là cạnh huyền, $AH$ là cạnh góc vuông nên $AB> AH$
Xét tam giác $ACH$ vuông tại $H$ có $AC$ là cạnh huyền, $AH$ là cạnh góc vuông nên $AC> AH$
Hình vẽ: