Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Từ a + 5 < b + 5
=> a + 5 + (-5) < b + 5 + (-5) (cộng hai vế với -5)
=> a < b
a)từ a+5<b+5 ta cộng -5 vào 2 vế được a<b
b)từ -3a>-3b ta nhân 2 vế với -1/3 (tức là chia cả 2 vế cho -3) và -3a . -1/3< -3b . -1/3 sẽ được a<b

1. \(a< b\Leftrightarrow2a< 2b\Leftrightarrow2a+1< 2b+1\)
\(a< b\Leftrightarrow-3a>-3b\Leftrightarrow-3a>-3b-1\)
2.\(a>b>0\Leftrightarrow a.\frac{1}{ab}>b.\frac{1}{ab}\Leftrightarrow\frac{1}{b}>\frac{1}{a}\Leftrightarrow\frac{1}{a}< \frac{1}{b}\)

a)Vì a<b=>2a<2b
=>2a+5<2b+5
b)Vì a<b=>-10a>-10b
=>2-10a>2-10b
c)Vì a<b=>7a<7b
=>7a-3<7b-3(1)
Vì -3<-1=>7b-3<7b-1(2)
Từ (1) và (2)=>đpcm
d)Vì a<b=>\(-\dfrac{a}{3}< -\dfrac{b}{3}\)
=>\(3-\dfrac{a}{3}>3-\dfrac{b}{3}\)(3)
Vì 3>1=>\(3-\dfrac{b}{3}>1-\dfrac{b}{3}\)(4)
Từ (3) và (4)=> đpcm
a, Ta có: a < b \(\Rightarrow\) 2a < 2b \(\Rightarrow\) 2a + 5 < 2b + 5
b, Ta có: a < b \(\Rightarrow\) -10a > -10b (đổi dấu) \(\Rightarrow\) 2 + (-10a) > 2 + (-10b) \(\Leftrightarrow2-10a>2-10b\)
c, Ta có: a < b \(\Rightarrow\)7a < 7b
Lại có: -3 < -1
\(\Rightarrow\) 7a + (-3) < 7a + (-1) \(\Leftrightarrow\) 7a - 3 < 7b - 1
d, Ta có: a < b \(\Rightarrow-\dfrac{a}{3}>-\dfrac{b}{3}\)(đổi dấu)
Lại có: 3 > 1
\(\Rightarrow3+\left(-\dfrac{a}{3}\right)>1+\left(-\dfrac{b}{3}\right)\Leftrightarrow3-\dfrac{a}{3}>1-\dfrac{b}{3}\)

Bài 1:
Áp dụng BĐt cauchy dạng phân thức:
\(\dfrac{1}{2x+y}+\dfrac{1}{x+2y}\ge\dfrac{4}{3\left(x+y\right)}\)
\(\Rightarrow\left(3x+3y\right)\left(\dfrac{1}{2x+y}+\dfrac{1}{x+2y}\right)\ge\left(3x+3y\right).\dfrac{4}{3x+3y}=4\)
dấu = xảy ra khi 2x+y=x+2y <=> x=y
Bài 2:
ta có: \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{1}{d}\ge\dfrac{4^2}{a+b+c+d}=\dfrac{16}{a+b+c+d}\)(theo BĐt cauchy-schwarz)
\(\Rightarrow\dfrac{1}{a+b+c+d}\le\dfrac{1}{16}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{1}{d}\right)\)
Áp dụng BĐT trên vào bài toán ta có:
\(A=\dfrac{1}{2a+b+c}+\dfrac{1}{a+2b+c}+\dfrac{1}{a+b+2c}\le\dfrac{1}{16}\left(\dfrac{2}{a}+\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{1}{a}+\dfrac{2}{b}+\dfrac{1}{c}+\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{2}{c}\right)\)\(A\le\dfrac{1}{16}.4\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)=\dfrac{1}{4}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\)
......
dấu = xảy ra khi a=b=c
Bài 2:
Áp dụng BĐT cauchy cho 2 số dương:
\(a^2+1\ge2a\)
\(\Leftrightarrow\dfrac{a}{a^2+1}\le\dfrac{a}{2a}=\dfrac{1}{2}\)
thiết lập tương tự:\(\dfrac{b}{b^2+1}\le\dfrac{1}{2};\dfrac{c}{c^2+1}\le\dfrac{1}{2}\)
cả 2 vế các BĐT đều dương ,cộng vế với vế,ta có dpcm
dấu = xảy ra khi a=b=c=1


Ta có:
\(\frac{1}{a}+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge\frac{16}{2a+b+c}\)(1)
Tương tự ta có:
\(\hept{\begin{cases}\frac{1}{a}+\frac{1}{b}+\frac{1}{b}+\frac{1}{c}\ge\frac{16}{a+2b+c}\left(2\right)\\\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{c}\ge\frac{16}{a+b+2c}\left(3\right)\end{cases}}\)
Cộng (1), (2), (3) vế theo vế ta được
\(16\left(\frac{1}{2a+b+c}+\frac{1}{a+2b+c}+\frac{1}{a+b+2c}\right)\le4\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)=16\)
\(\Leftrightarrow\frac{1}{2a+b+c}+\frac{1}{a+2b+c}+\frac{1}{a+b+2c}\le1\)

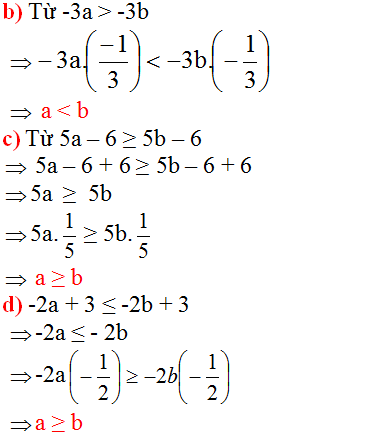
Ta có: - 2a - 8 < - 2b – 8 nên: -2a - 8 + 8 < - 2b – 8 + 8 hay -2a < - 2b
Nhân cả 2 vế bất đẳng thức với -1/2 < 0 ta được: a > b
Chọn đáp án A