Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hệ vô nghiệm khi và chỉ khi:
\(\dfrac{m}{n}=-\dfrac{2}{5}\ne-\dfrac{2}{13}\)
\(\Rightarrow2n+5m=0\)
Kêyt hợp với \(2m-n=9\) ta được:
\(\left\{{}\begin{matrix}5m+2n=0\\2m-n=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5m+2n=0\\4m-2n=18\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}9m=18\\4m-2n=18\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=2\\n=-5\end{matrix}\right.\)

a) x 2 - 7x + 5 = 0
Δ = 7 2 - 4.1.5 = 49 - 20 = 29 > 0
⇒ Phương trình đã cho có 2 nghiệm phân biệt
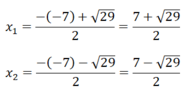
Vậy hệ phương trình đã cho có tập nghiệm
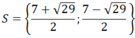


Cô làm câu b thôi nhé :)
Ta có hệ \(\hept{\begin{cases}mx+4y=10-m\\x+my=4\end{cases}}\Leftrightarrow\hept{\begin{cases}m\left(4-my\right)+4y=10-m\\x=4-my\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(4-m^2\right)y=10-5m\left(1\right)\\x=4-my\end{cases}}\)
Với \(4-m^2=0\Leftrightarrow m=2\) hoặc \(m=-2\)
Xét m =2, phương trình (1) tương đương 0.x = 0. Vậy hệ phương trình có vô số nghiệm dạng \(\left(4-2t;t\right)\)
Xét m = -2, phương trình (1) tương đương 0.x = 20. Vậy hệ phương trình vô nghiệm.
Với \(4-m^2\ne0\Leftrightarrow m\ne2\) và \(m\ne-2\), phương trình (1) tương đương \(y=\frac{10-5m}{4-m^2}=\frac{5}{2+m}\)
Từ đó : \(x=\frac{8-m}{2+m}\)
Kết luận:
+ m = 2, hệ phương trình có vô số nghiệm dạng \(\left(4-2t;t\right)\)
+ m = - 2, hệ phương trình vô nghiệm.
+ \(m\ne2;m\ne-2\) hệ có 1 nghiệm duy nhất \(\hept{\begin{cases}x=\frac{8-m}{2+m}\\y=\frac{5}{2+m}\end{cases}}\)
Chúc em học tập tốt :)


Thay x = -3, y = 31/5 vào vế trái của phương trình (2), ta được:
VT = -3.(-3) + 2.31/5 = 9 + 62/5 = 107/5 ≠ 22 = VP
Vậy (x; y) = (-3; 31/5 ) không phải là nghiệm của phương trình (2).
Hệ phương trình đã cho vô nghiệm.

bn có máy tính thì vào eqn rùi vào un.. j đó nhấn 2 rùi giải thui ak, mk mới lớp 6 nhưng mk bít cách giải hệ phương trình 2 ẩn rùi

Thì phương trình thứ 2 các hệ số của x, y đều gấp 2 lần pt 1 mà VP phương trình 2 không gấp đôi VT pt 1 nên vô nghiệm chớ sao
Cả 2 chữ đều là VP hết nha. Viết láu táu nên ghi nhầm thành VT. Sorry nhá