Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Số phần tử của không gian mẫu:
![]()
Gọi A là biến cố “nhóm được chọn có cả nam và nữ, đồng thời mỗi khối có 1 học sinh nam”
⇒ số phần tử của biến cố A là: ![]()
![]() .
.

Đáp án :C
Nhà trường có hai cách chọn:
Trường hợp 1. Chọn 1 học sinh nam. có 307 cách
Trường hợp 2. Chọn 1 học sinh nữ. Có 326 cách
Vậy, có 307 + 326 = 633 cách chọn một học sinh tham dự cuộc thi trên.

Ta có các khả năng sau
Đội tình nguyện chỉ có Khánh mà không có Oanh
Số cách chọn chính bằng số cách chọn 3 học sinh từ 14 học sinh lớp A (vì đã chọn Khánh) và 3 học sinh từ 9 (vì đã loại Oanh) học sinh lớp B nên số cách chọn bằng: ![]()
Đội tình nguyện chỉ có Oanh mà không có Khánh
Số cách chọn bằng: ![]()
Vậy số cách chọn là: ![]()
Chọn C.

Gọi A là biến cố : "4 học sinh được chọn có đủ học sinh giỏi, học sinh khá và học sinh trung bình"
Số phần tử không gian mẫu \(\left|\Omega\right|=C^4_{33}=40920\)
Ta có các trường hợp được chọn sau :
(1) Có 2 học sinh giỏi, 1 học sinh khá và 1 học sinh trung bình. Số cách chọn là : \(C^2_{10}.C^1_{11}.C^1_{12}=5940\).
(2)Có 1 học sinh giỏi, 2 học sinh khá và 1 học sinh trung bình. Số cách chọn là : \(C^1_{10}.C^2_{11}.C^1_{12}=6600\).
(3)Có 1 học sinh giỏi, 1 học sinh khá và 2 học sinh trung bình. Số cách chọn là : \(C^1_{10}.C^1_{11}.C^2_{12}=7260\).
Ta được \(\left|\Omega_A\right|=5940+6600+7260=19800\)
Do đó : \(P\left(A\right)=\frac{\left|\Omega_A\right|}{\left|\Omega\right|}=\frac{15}{31}\)

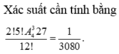

2*14*13*12=4368 cách
4*13*12*3=1872