Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi chiều cao của tháp là AB, bóng của tòa tháp trên mặt đất là AC.
Theo đề, ta có: AB\(\perp\)AC tại A, \(\widehat{C}=45^0\); AC=30m
Xét ΔABC vuông tại A có \(tanC=\dfrac{AB}{AC}\)
=>\(\dfrac{AB}{30}=tan45=1\)
=>AB=30(m)
=>Chọn A

\(\left[{}\begin{matrix}\\\\\\\end{matrix}\right.\prod\limits^{ }_{ }\int_{ }^{ }dx\sinh_{ }^{ }⋮\begin{matrix}&&&\\&&&\\&&&\\&&&\\&&&\\&&&\end{matrix}\right.\Cap\begin{matrix}&&\\&&\\&&\\&&\\&&\\&&\end{matrix}\right.\)

bạn hỏi nhiều quá , các bạn nhìn vào ko biết trả lời sao đâu !!!
rối mắt quá mà viết dày nên bài nọ xọ bài kia mình ko trả lời được cho dù biết rất rõ

Ý cuối câu b.
Sử dụng công thức tính diện tích tam giác ABC. Ta có:
\(\frac{1}{2}AB.\sin\widehat{A}.AC=\frac{1}{2}AH.BC\)
=> \(AB.\sin\widehat{A}.AC=AH.BC\)
Ta đã tính được: \(AH=3\sqrt{3};AB=6;AC=2\sqrt{13};MN=\frac{18\sqrt{13}}{13};BC=8\) ( để tính MN sử dụng tam giác đồng dạng ở câu b ý 1 nha)
=> \(\sin\widehat{A}.AH=\frac{AH^2.BC}{AB.AC}=\frac{18\sqrt{13}}{13}=MN\)

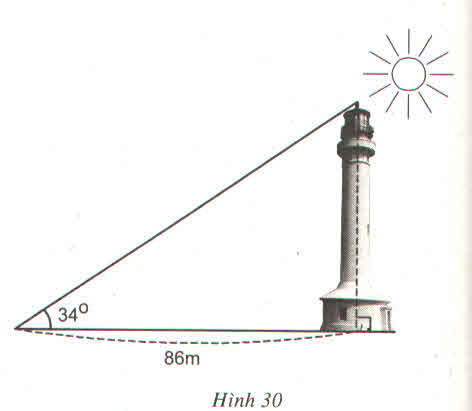
Gọi a là chiều cao của tháp, ta có:
\(\tan34\) = \(\dfrac{c.đối}{c.kề}\)= \(\dfrac{a}{86}\)
\(\Rightarrow a=\) \(\tan34.86\) \(\approx\) 58m
Vậy chiều cao của tháp là 58m