Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\lambda = v/f = 80/20 = 4cm.\)
\(\triangle \varphi = \pi-0=\pi.\)
Nhận xét: \(BM-AM=(BI+IM)-(AI-IM)=2MI\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{BM-AM}{\lambda}-\frac{\triangle\varphi}{2\pi})|\\=|2a\cos\pi(\frac{2MI}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{6}{4}-\frac{\pi}{2\pi})| = |-2a|=2a=10 mm.\)

Chọn đáp án D
λ = v f = 60 c m u = 2 A cos π ( d 1 - d 2 ) λ cos 10 π t - π ( d 1 - d 2 ) λ = 4 cos π 12 cos 10 π t - 7 π 12

Bước sóng \(\lambda = v/f = 1/25 = 0.04m = 4cm.\)
Độ lệch pha giữa hai nguồn sóng là \(\triangle\varphi= \varphi_2-\varphi_1 = \frac{5\pi}{6}+\frac{\pi}{6} = \pi.\)
Biên độ sóng tại điểm M là \( A_M = |2a\cos\pi(\frac{10-50}{4}-\frac{\pi}{2\pi})| =0.\)

Đáp án: A
HD Giải: λ = 80 2 π 100 π = 1,6cm
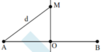
M cùng pha với nguồn A nên MA = d = (được rút ra từ phương trình sóng tại M với d1 = d2 = d)
Ta có điều kiện MA > AO = AB/2 nên
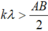
<=> 1,6k > 6
<=> k > 3,75
MA nhỏ nhất nên chọn k = 4
MA = 4.1,6 = 6,4 cm

\(\lambda = v/f = 0.8/100 = 0.008m = 0.8cm.\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{0}{\lambda}-\frac{0}{2\pi})| = |2a| = 2a.\)
\(u_M = A_M\cos(2\pi ft - \pi\frac{d_2+d_1}{\lambda}+\frac{\varphi_1+\varphi_2}{2})\\= A_M\cos(200\pi t - \pi\frac{8+8}{0.8}+\frac{0}{2})= 2a\cos(200\pi t - \pi\frac{8+8}{0.8})= 2a\cos(200\pi t-20\pi)=2a\cos(200\pi t)\)
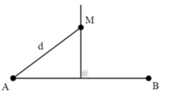



Em xem thêm lý thuyết giao thoa sóng tại đây: Giao thoa sóng | Học trực tuyến
Áp dụng công thức tổng hợp giao thoa:
\(u=2a\cos(\dfrac{\pi(d_2-d_1)}{\lambda}).\cos(\omega t -\dfrac{\pi(d_2+d_1)}{\lambda})\)
Ta có:
Câu 1:
\(\lambda = v/f=1/10=0,1m=10cm\)
M là trung điểm AB thì cách A, B là 5cm
\(\Rightarrow u=2.5\cos(\dfrac{\pi(5-5)}{10}).\cos(20\pi t -\dfrac{\pi(5+5)}{10})\)
\(\Rightarrow u=10.\cos(20\pi t -\pi)(cm)\)
Câu 2:
Bước sóng: \(\lambda = v/f = 3/5=0,6m=60cm\)
\(\Rightarrow u=2.2\cos(\dfrac{\pi(20-15)}{60}).\cos(10\pi t -\dfrac{\pi(15+20)}{60})\)
= ....