Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D E
Kéo dài \(DA,CB\)cắt nhau tại \(E\).
Xét tam giác \(CDE\)có:
\(\widehat{EDC}=\widehat{ECD}\)(vì \(ABCD\)là hình thang cân)
suy ra \(\Delta CDE\)cân tại \(E\).
\(\Rightarrow ED=EC\)
\(AB//CD\Rightarrow\widehat{EAB}=\widehat{EDC},\widehat{EBA}=\widehat{ECD}\)(góc đồng vị)
suy ra \(\widehat{EAB}=\widehat{EBA}\)
\(\Rightarrow\Delta EAB\)cân tại \(E\)
\(\Rightarrow EA=EB\)
Suy ra \(ED-EA=EC-EB\Leftrightarrow AD=BC\).
Xét tam giác \(ADC\)và tam giác \(BCD\)có:
\(AD=BC\)
\(\widehat{ADC}=\widehat{BCD}\)
\(CD\)chung
suy ra \(\Delta ADC=\Delta BCD\left(c.g.c\right)\)
\(\Rightarrow AC=BD\)(hai cạnh tương ứng)

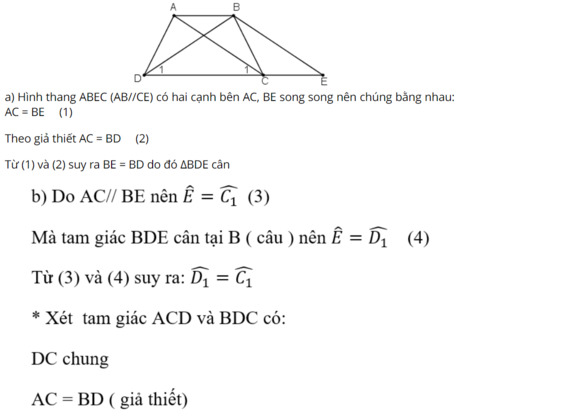
Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại E.
Ta có:
Góc ACD = góc BED (tính chất góc hình bình hành)
mà gócBDE = gócBED ( BDE là tam giac cân tại B)
=> góc ACD= góc BDC
xét 2 tam giác ACD và tam giác BDC có:
+ AC = BD ( gt)
+ góc ACD = góc BDC
+có cùng cạnh CD
=> tam giác ACD = tam giác BDC ( cạnh,góc,cạnh)
xét hình thang ABCD:
AD = BC vì tam giác ACD = tam giác BDC
=> ABCD là hình thang cân.
Vậy hình thang có hai đường chéo bằng nhau là hình thang cân.(đpcm)

Không nhé bạn, đây chỉ là tính chất của hình thang cân thôi

Giả sử hình thang là ABCD,
Qua B kẻ đường thẳng với AC cắt DC tại E
a)Ta có ACD=BAC (AB//CD)
mà ACD =BEC =>BEC=BAC
Xét tam giac ABC va tam giác ECB
+BC chung
+ACB=EBC(so le trong)
+BEC=BAC(cm trên )
=>tam giac ABC =tam giac ECB
=>BDC=BEC
mà BEC=ACD(đồng vị)=>ACD=BDC
xét tam giac ACD va tam giac BDC,ta có :
+DC chung
+ACD=BDC
+AC=BD(gt)
=>tam giac ACD=tam giác BDC
=>ADC=BCD
=>ABCD la hình thang cân (dfcm)

1.
O A B D C E
+) Tứ giác ABCD kà hình thang cân => góc ADC = BCD và AD = BC
=> tam giác ODC cân tại O => OD = OC
mà AD = BC => OA = OB
+) tam giác ODB và OCA có: OD = OC; góc DOC chung ; OB = OA
=> Tam giác ODB = OCA (c - g - c)
=> góc ODB = OCA mà góc ODC = OCD => góc ODC - ODB = OCD - OCA
=> góc EDC = ECD => tam giác EDC cân tại E => ED = EC (2)
Từ (1)(2) => OE là đường trung trực của CD
=> OE vuông góc CD mà CD // AB => OE vuông góc với AB
Tam giác OAB cân tại O có OE là đường cao nên đồng thời là đường trung trực
vậy OE là đường trung trực của AB

hình đâu bạn
Câu 1: trang 73 sách giáo khoa 8 tập 1
Câu 2: trang 73 sách giáo khoa 8 tập 1