Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn đáp án C.
Vì x, y ,z > 0 nên x + y > 0; y + z > 0 và x + z > 0
Ta có:
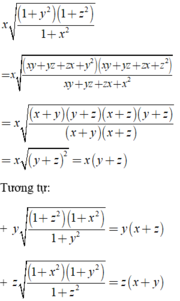
Khi đó
A = x(y + z) + y(x + z) + z(x + y)
= xy + xz + xy + yz + xz + zy = 2(xy + yz + zx) = 2

a/ Gọi x là số ong thợ, y là số ong đực thì y = 0,02x
Ta có 32x + 16 x 0,02x =155136; x = 4800; y = 96
b/ Tổng số trứng đẻ là (4800x100/80) + (96x100/60) = 6160
c/ Tổng số nhiễm sắc thể bị tiêu biến
- Số trứng thụ tinh đẻ ra: 4800 x 100/80 = 6000 trứng
- Số tinh trùng không thụ tinh: (6000 x 100) – 6000 = 594000
- Số trứng không thụ tinh đẻ ra: 96 x 100/60 = 160 trứng
- Số trứng không thụ tinh không nở: 160 – 96 = 64
- Số trứng thụ tinh không nở: 6000 – 4800 = 1200
- Tổng số nhiễm sắc thể bị tiêu biến: (32 x 1200) + 16(64 + 594000) = 9543424 NST

Lời giải:
a)
Ta có: \(MP=MQ\) (tính chất 2 tiếp tuyến cắt nhau)
\(OP=OQ=R\)
\(\Rightarrow MO\) là đường trung trực của $PQ$
\(\Rightarrow MO\perp PQ \rightarrow \widehat{OKI}=90^0\)
Xét tam giác $OKI$ và $OHM$ có:
\(\left\{\begin{matrix} \text{chung góc O}\\ \widehat{OKI}=\widehat{OHM}=90^0\end{matrix}\right.\Rightarrow \triangle OKI\sim \triangle OHM(g.g)\)
\(\Rightarrow \frac{OI}{OK}=\frac{OM}{OH}\Rightarrow OI.OH=OK.OM\) (đpcm)
b)
Vì $MQ$ là tiếp tuyến $(O)$ nên $MQ\perp OG$
Xét tam giác vuông $MQO$, có đường cao $QK$ ứng với cạnh huyền $MO$, ta áp dụng hệ thức lượng trong tam giác vuông thì có: \(OK.OM=OQ^2=R^2\)
Kết hợp với kết quả phần a suy ra \(OI.OH=R^2\)
$O$ cố định, $xy$ cố định nên $H$ cố định, suy ra $OH$ cố định
Vậy $R^2$ và $OH$ cố định, do đó $OI$ cố định, kéo theo $I$ là điểm cố định.
Hiển nhiên $I\in PQ$ nên $PQ$ luôn đi qua điểm cố định $I$ khi $M$ thay đổi.
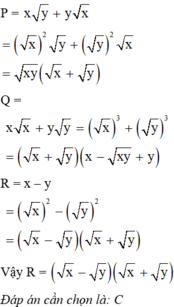
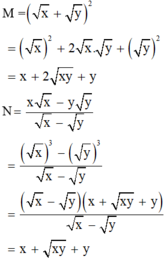
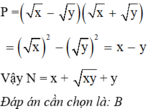

Chọn B
ý bạn là đáp án thứ 2 hả?