K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 6 2017
Ta có |x - 3,5| + |y - 1,3| = 0
Mà : |x - 3,5| \(\ge0\forall x\in R\)
|y - 1,3| \(\ge0\forall x\in R\)
Suy ra : |x - 3,5| = |y - 1,3| = 0
\(\Leftrightarrow\orbr{\begin{cases}x-3,5=0\\y-1,3=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=3,5\\y=1,3\end{cases}}\)
14 tháng 12 2019
|x-3,5| + |y-1,3|=0
Do |x-3,5| lớn hơn hoặc bằng 0; |y-1,3| lớn hơn hoặc bằng 0 nên |x-3,5|= 0 và |y-1,3|=0
* |x-3,5|= 0
=> x-3,5=0
x=0+3,5
x=3,5
* |y-1,3|=0
=> y-1,3=0
y=1,3+0
y=1,3
Vậy x=3,5
y=1,3
VM
14 tháng 12 2019
\(\left|x-3,5\right|+\left|y-1,3\right|=0\)
Ta có:
\(\left\{{}\begin{matrix}\left|x-3,5\right|\ge0\\\left|y-1,3\right|\ge0\end{matrix}\right.\forall x,y.\)
\(\Rightarrow\left|x-3,5\right|+\left|y-1,3\right|=0\)
\(\Rightarrow\left\{{}\begin{matrix}\left|x-3,5\right|=0\\\left|y-1,3\right|=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x-3,5=0\\y-1,3=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=3,5\\y=1,3\end{matrix}\right.\)
Vậy \(\left(x;y\right)\in\left\{3,5;1,3\right\}.\)
Chúc bạn học tốt!
LK
3
16 tháng 8 2021
c: Ta có: \(\left|\dfrac{1}{2}x-2\right|-\left|x+3\right|=0\)
\(\Leftrightarrow\left|\dfrac{1}{2}x-2\right|=\left|x+3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}x-2=x+3\\\dfrac{1}{2}x-2=-x-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x\cdot\dfrac{-1}{2}=5\\x\cdot\dfrac{3}{2}=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-10\\x=-\dfrac{2}{3}\end{matrix}\right.\)
MC
1
22 tháng 8 2015
ta có vì |3x-4|>0
|3y+5|>0
Vậy suy ra
|3x-4|=0 và |3y+5|=0
3x-4=0 suy ra x=4/3
3y+5=0 suy ra y=5/3
cái sau cũng làm giống vậy
VM
1 tháng 10 2019
\(\left|x-3,5\right|+\left|y-1,3\right|=0\)
Ta có:
\(\left\{{}\begin{matrix}\left|x-3,5\right|\ge0\\\left|y-1,3\right|\ge0\end{matrix}\right.\forall xy.\)
\(\Rightarrow\left|x-3,5\right|+\left|y-1,3\right|=0\)
\(\Rightarrow\left\{{}\begin{matrix}x-3,5=0\\y-1,3=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=0+3,5\\y=0+1,3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=3,5\\y=1,3\end{matrix}\right.\)
Vậy \(\left(x;y\right)\in\left\{3,5;1,3\right\}.\)
Chúc bạn học tốt!
1 tháng 10 2019
Các bạn giúp mk nhanh vs nhá, chiều mai mk cần. cảm ơn trước
MC
2
BT
24 tháng 9 2016
a) |3x - 4| + |3y+5| = 0
=> 3x -4= 0 => x= 4/3
và 3y + 5 = 0 => y = -5/3
Vậy x= 4/3; y= -5/3
b) |x-3,5| + |4-x| = 0
=> x- 3,5 =0 => x=3,5
và 4-x=0 => x=4
Vậy không tìm được x thỏa mãn
U
8 tháng 8 2018
\(\left|3x-4\right|+\left|3y+5\right|=0\)
vì :
\(\left|3x-4\right|\ge0\)
\(\left|3y+5\right|\ge0\)
nên :
\(\hept{\begin{cases}\left|3x-4\right|=0\\\left|3y+5\right|=0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}3x-4=0\\3y+5=0\end{cases}\Rightarrow\hept{\begin{cases}x=\frac{4}{3}\\y=\frac{-5}{3}\end{cases}}}\)
vậy_
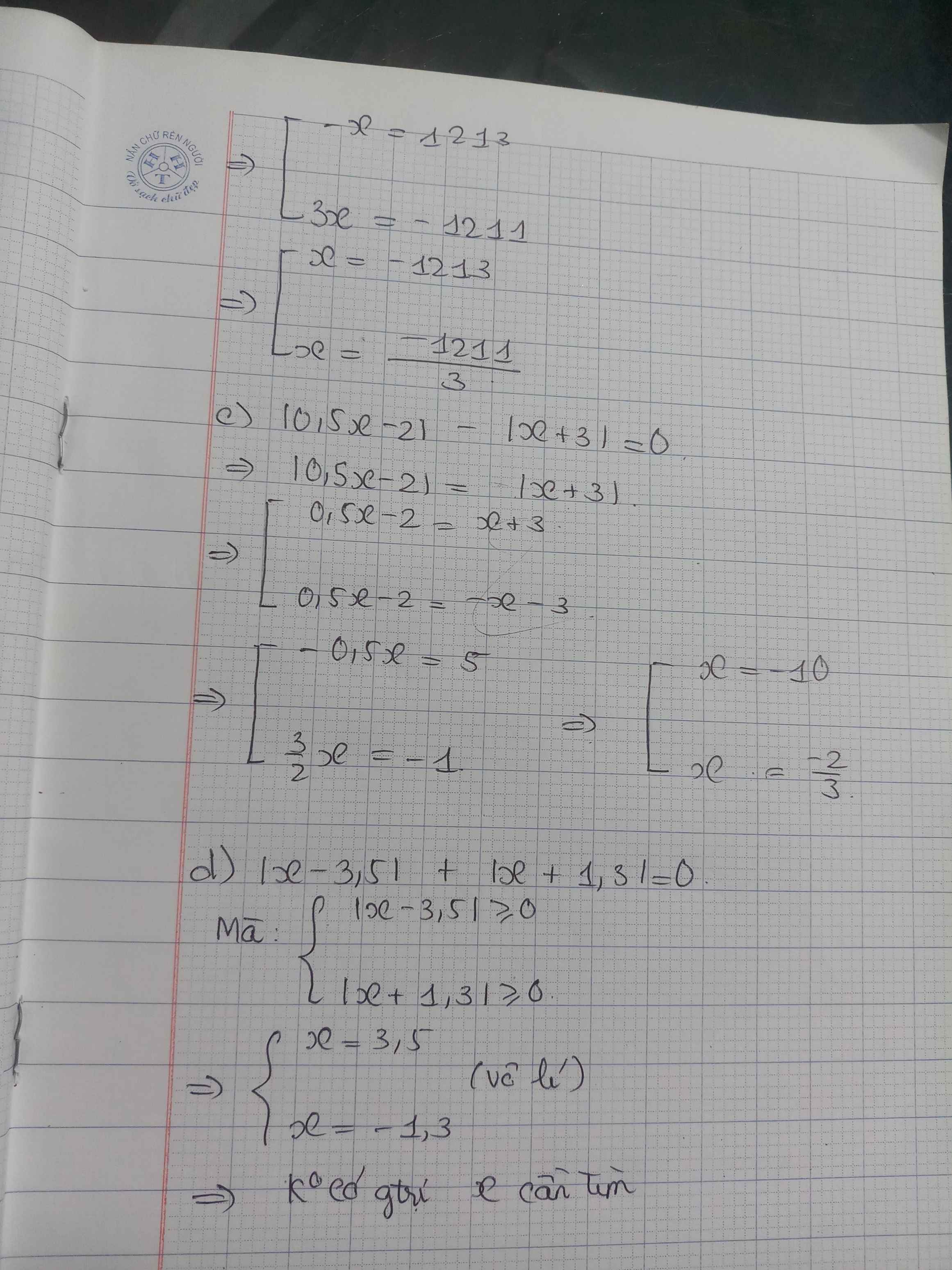
Với mọi giá trị của x;y ta có:
\(\left|x-3,5\right|+\left|y-1,3\right|\ge0\)
Để \(\left|x-3,5\right|+\left|y-1,3\right|=0\) thì
\(\left\{{}\begin{matrix}\left|x-3,5\right|=0\\\left|y-1,5\right|=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=3,5\\y=1,5\end{matrix}\right.\)
Vậy.......
Chúc bạn hcọ tốt!!!