Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo định lý Pythagoras, ta có công thức: c^2 = a^2 + b^2, trong đó c là cạnh huyền (BC), a và b là hai cạnh góc vuông (MB và MC).
Với MB = 2m và cây sào cao 6m, ta có MC = 6m - 2m = 4m.
Áp dụng công thức Pythagoras, ta có: BC^2 = MB^2 + MC^2 = 2^2 + 4^2 = 4 + 16 = 20.
Do đó, khoảng cách BC là căn bậc hai của 20: BC = √20 ≈ 4.47m (làm tròn đến hai chữ số thập phân).

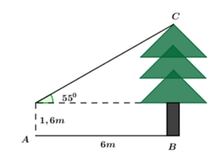
Gọi tam giác tại bởi phần thân cây bị gãy với phần cây còn lại và mặt đất là △ ABC vuông tại A. Ta có
cos 20 = 7.5 / cạnh huyền
⇒ cạnh huyền = \(\dfrac{7,5}{cos20}\)\(\approx\) 8 ( m )
Áp dụng định lý Py-ta-go ta có:
phần bị gãy của cây cau là : \(\sqrt{8^2-7,5^2}\) = 2.78 ( m )
⇒ Chiều cao cây cau lúc đầu là : 8 + 2.78 =10.78 ( m )

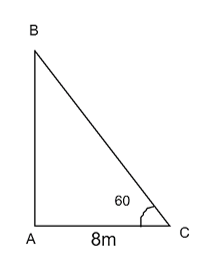
tanˆBCA=ABAC=AB8⇒tan600=AB8⇒AB=8√3(m)≈13,86mtan���^=����=��8⇒tan600=��8⇒��=83(�)≈13,86�
Vậy cây cổ thụ có chiều cao khoảng 13,86 m.

Với góc nhìn tạo với phương nằm ngang là 42 độ, ta có:
tan(42°) = h / 15
Để tìm giá trị của h, ta cần giải phương trình trên để tìm giá trị của h.
tan(42°) = h / 15
h = tan(42°) * 15
Sử dụng máy tính, ta tính được:
h ≈ 15.7m
Vậy, chiều cao của cây là khoảng 15.7m.

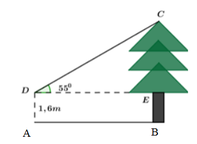
Đặt các điểm D, E như hình vẽ.
Xét CDE vuông tại E ta có:
![]()
Chiều cao của cây là BC = CE + BE = 8,57 + 1,6 = 10,17m
Đáp án cần chọn là: D