K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
10 tháng 2 2018
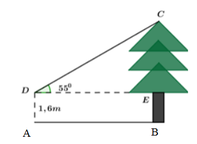
Đặt các điểm D, E như hình vẽ.
Xét CDE vuông tại E ta có:
![]()
Chiều cao của cây là BC = CE + BE = 8,57 + 1,6 = 10,17m
Đáp án cần chọn là: D

CJ
29 tháng 8 2023
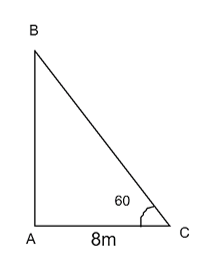
tanˆBCA=ABAC=AB8⇒tan600=AB8⇒AB=8√3(m)≈13,86mtan���^=����=��8⇒tan600=��8⇒��=83(�)≈13,86�
Vậy cây cổ thụ có chiều cao khoảng 13,86 m.
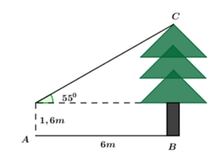

Theo định lý Pythagoras, ta có công thức: c^2 = a^2 + b^2, trong đó c là cạnh huyền (BC), a và b là hai cạnh góc vuông (MB và MC).
Với MB = 2m và cây sào cao 6m, ta có MC = 6m - 2m = 4m.
Áp dụng công thức Pythagoras, ta có: BC^2 = MB^2 + MC^2 = 2^2 + 4^2 = 4 + 16 = 20.
Do đó, khoảng cách BC là căn bậc hai của 20: BC = √20 ≈ 4.47m (làm tròn đến hai chữ số thập phân).
bạn ơi, sao MC lại bằng 6-2, bạn giải thích ro hơn giúp mình