Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

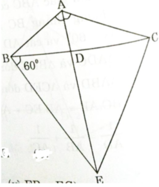
a) Xét ΔADC ∼ ΔBDE có:
∠DBE = ∠CAD ( = 60o)
∠BDE = ∠CDA (đối đỉnh)
⇒ ΔADC ∼ ΔBDE (g.g)
Xét ΔEBD và ΔEAB có:
∠BEA chung;
∠EBD = ∠BAE = 60o
⇒ ΔEBD ∼ ΔEAB (g.g)
![]()
b) Ta có ΔADC ∼ ΔBDE (cmt)
![]()
Lại có ∠ADB = ∠EDC (đối đỉnh)
Do đó ΔADB ∼ ΔCDE (c.g.c)
⇒ ∠BCE = ∠BAD = 60o
Vậy ΔEBC đều (∠EBC = ∠BCE = 60o )
c) Vì AD là phân giác của ∠BAC (gt) ta có:
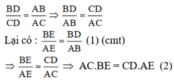
Từ (1) ta có AE.BD = BE.AB = EC.AB (vì EB = EC)
Hay EC.AB = AE.BD (3)
Công (2) và (3): AB.EC + AC.BE = AE(CD + BD) = AE.BC (đpcm)
d) Ta có: AE.BC = AB.EC + AC.BE
= AB.BC + AC.BC (vì BC = EC = BE)
= BC(AB + AC) ⇒ AE = AB + AC (*)
Mặt khác: Xét ΔADC và ΔABE có: ∠CAD = ∠BAE = 60o ; ∠ACD = ∠AEB (cmt)
⇒ ΔADC ∼ ΔABE (g.g)
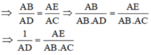
Theo (*) ta có:
![]()

a: Xét ΔABE và ΔADC có
góc BAE=góc DAC
góc AEB=góc ACD
=>ΔABE đồng dạng với ΔADC
b: ΔABE đồng dạng với ΔADC
=>AE/AC=AB/AD
=>AE*AD=AB*AC=BE^2

a) Xét tam giác MBD và tam giác MAB:
\(\widehat{DMB}chung.\)
\(\widehat{DBM}=\widehat{BAM}\left(\widehat{CBx}=\widehat{BAD}\right).\)
=> Tam giác MBD \(\sim\) Tam giác MAB (g - g).
bạn tự vẽ hình nhé a)Vì AD là p/g của \(\widehat{BAC}\)nên \(\widehat{CAD}=\widehat{DAB}=\frac{1}{2}\widehat{BAC}\Rightarrow\widehat{CAD}=\frac{1}{2}\times120=60\)
Xét \(\Delta ADC\)và \(\Delta BDE\)có \(\widehat{ADC}=\widehat{BDE}\)(đối đỉnh); \(\widehat{DAC}=\widehat{DBE}\)(=60)
\(\Leftrightarrow\Delta ADC\infty\Delta BDE\left(g.g\right)\Rightarrow\frac{AD}{BD}=\frac{CD}{DE}\Rightarrow AD.DE=BD.DC\) (đfcm)
b)Xét \(\Delta ADB\) và \(\Delta CDE\) có: \(\widehat{ADB}=\widehat{CDE}\) (đối đỉnh); \(\frac{AD}{BD}=\frac{CD}{DE}\left(cmt\right)\)
\(\Rightarrow\Delta ADB\infty\Delta CDE\left(c.g.c\right)\) (đfcm)
c) trên AE lấy I sao cho AI=AB\(\Rightarrow\Delta AIB\)cân tại A có \(\widehat{IAB}=60\Rightarrow\Delta AIB\) đều \(\Rightarrow\widehat{ABI}=60\Rightarrow\widehat{ABD}=\widehat{IBE}\) Xét \(\Delta ABC=\Delta IBE\left(c.g.c\right)\Rightarrow AC=IE\Rightarrow AB+AC=AI+IE=AE\left(1\right)\)ta có \(AB.EC+AC.BE=AB.BC+AC.BC=BC.\left(AB+AC\right)\left(2\right)\)thay (1) vào (2) ta được \(AB.EC+AC.BE=BC.AE\left(đfcm\right)\)