K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

12 tháng 7 2021
a) Xét ΔABE và ΔADC có
\(\widehat{BAE}=\widehat{DAC}\)(hai góc đối đỉnh)
\(\widehat{AEB}=\widehat{ACD}\)(ΔDBE\(\sim\)ΔDAC)
Do đó: ΔABE\(\sim\)ΔADC(g-g)

TL
31 tháng 1 2019
HÌNH TỰ KẺ NHA
1a) trong tam giác ADB có ADC là góc ngoài tại đỉnh D
=>góc ADC = góc BAD + góc ABD
mà góc BAD = góc DBE
=>góc ADC = góc ABD + góc DBE
=>góc ADB = góc ABE
Xét tam giác ADC va tam giác ABE
Góc BAD = góc CAD(AD là p/g tại đỉnh A)
góc ABE = góc ADC(cmt)
=> tam giác ABE đồng dạng với tam giác ADC(g.g)
1b) Xét tam giac AEB và tam giác BED
góc E chung
góc DBE = góc DAB(gt)
=>tam giác ABE đồng dạng vói tam giác BDE(g.g)
=>BE/DE = AE/BE
=>BE.BE=DE.AE
hayBE^2=DE.AE
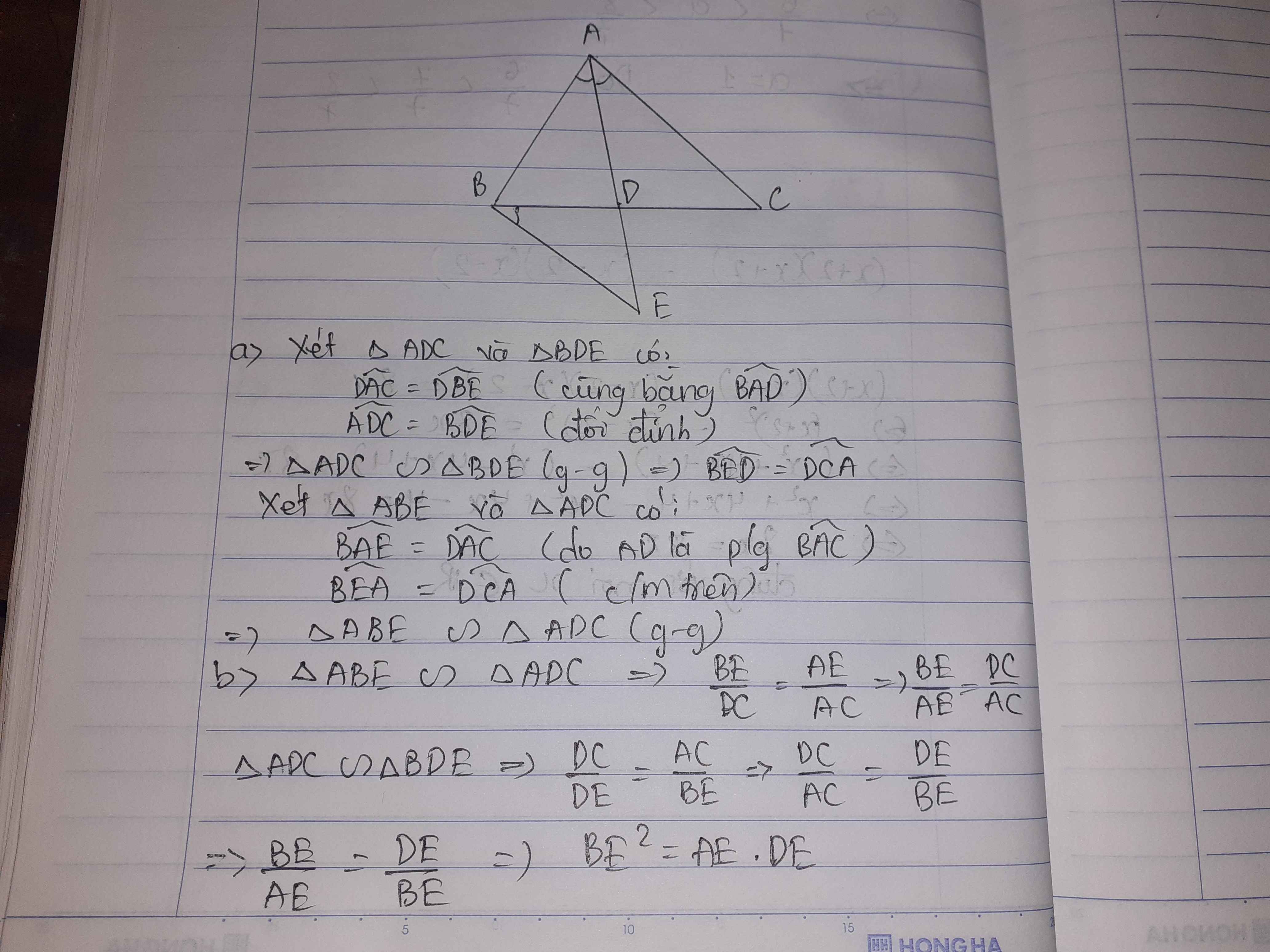
a: Xét ΔABE và ΔADC có
góc BAE=góc DAC
góc AEB=góc ACD
=>ΔABE đồng dạng với ΔADC
b: ΔABE đồng dạng với ΔADC
=>AE/AC=AB/AD
=>AE*AD=AB*AC=BE^2