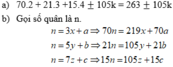Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tôi để hai chữ " Tôn Tử " trong dấu ngoặc kép, vì tôi không có tài liệu nào trong tay để quyết đoán bài thơ " Điểm Binh " trên là của Tôn Tử.
(Ý bài nầy là " Tôn Tử " biết chừng chừng số binh của mình. Muốn biết số binh chính xác, thì :
- Làm dấu hiệu thứ nhất - như phất một lần cây cờ - thì cứ 3 người lính đứng lại thành một nhóm, số lính còn lại không lập được một nhóm là 0, 1 hoặc 2 người ; số nầy sẽ nhân với 70.
- Làm dấu hiệu thứ hai, thì cứ 5 người lính đứng lại thành một nhóm, số lính còn lại không lập được một nhóm là 0, 1, 2, 3 hoặc 4 người ; số nầy sẽ nhân cho 21.
- Làm dấu hiệu thứ ba, thì cứ 7 người lính đứng lại thành một nhóm, số lính còn lại không lập được một nhóm là 0, 1, 2, 3, 4, 5 hoặc 6 người ; số nầy sẽ nhân cho 15.
Cọng tất cả 3 số vừa được nhân ở trên, và nếu cần thì cọng thêm, hoặc trừ ra 105, để được số binh chính xác.).
Ví dụ : Số binh là 437, và " Tôn Tử " biết chừng chừng là khoảng 400.
- Nếu sắp 3 người thành một nhóm, thì lẻ ra 2 người,
- Nếu sắp 5 người thành một nhóm, thì lẻ ra 2 người,
- Nếu sắp 7 người thành một nhóm, thì lẻ ra 3 người.
Và : (2 x 70) + (2 x 21) + (3 x 15) + 105 + 105 = (140 + 42 + 45) + 210 = 227 + 210 = 437.
Cái hay ở đây là chỉ dùng có 3 động tác đơn sơ và chỉ trong vài ba phút mà " Tôn Tử " đã biết được số binh chính xác của mình.
Chuyện bài toán trên là Phép Chia Euclide (1) về Số Học trong Tập Hợp Số Nguyên Z. Vậy ta có thể thay những số 3, 5, 7; 70, 21, 15; 105, trên, bằng những nhóm số khác như 2, 3, 5; 15, 10, 6; 30; hay 3, 5, 11; 55, 66, 45; 165 ; vân vân, nhưng theo tôi nhóm số 3, 5, 7; 70, 21, 15; 105 trên vẫn đơn giản hơn nhiều.
Ví dụ với nhóm số 2, 3, 5; 15, 10, 6; 30 :
Cũng lấy số binh trên 437.
- Nếu xếp 2 người thành một nhóm, thì lẻ ra 1 người,
- Nếu xếp 3 người thành một nhóm, thì lẻ ra 2 người,
- Nếu xếp 5 người thành một nhóm, thì lẻ ra 2 người.
Và (1 x 15) + (2 x 10) + (2 x 6) + (13 x 30) = (15 + 20 + 12) + 390 = 47 + 390 = 437.
Ở đây 47 phải cọng thêm 13 lần 30, (13 x 30 = 390).

( Ý bài này là " Tôn Tử" biết chừng chừng số binh của mình . Muốn biết sô chính xác thì:
- Làm dấu hiệu thứ nhất - như phất một lần cây cờ - thì cứ 3 người lính đứng lại thành một nhóm, số lính còn lại không lập được một nhóm là 0, 1 hoặc 2 người, số này sẽ nhân với 70.
- Làm dấu hiệu thứ 2 thì cư 5 người lính đứng lại thành một nhóm, số lính còn lại không lập được một nhóm là 0,1,2,3 hoặc 4 người, số này sẽ nhân với 21
- Làm dấu hiệu thứ ba, thì cứ 7 người lính đứng lại thành một nhóm, số lính còn lại không lập được một nhóm là 0,1,2,3,4,5 hoặc 6 người, số này sẽ nhân cho 15
Cộng tất cả 3 số vừa được nhân ở trên, và nếu cần thì cộng thêm, hoặc trừ ra 105, để được số bình chính xác )
Ví dụ: số bình là 437 và " tôn tử" biết chừng chừng là khoảng 400
- Nếu 3 người thanhg một nhóm, thì lẻ ra 2 người
- Nếu 5 người thành một nhóm thì lẻ ra 2 người
- Nếu 7 người thành một nhóm thi lẻ ra 3 người
Và : ( 2 x 70) + ( 2 x 21 )+ ( 3 x 15 )+ 105 + 105 = ( 140+ 42+ 45 ) + 210 = 227 + 210 = 437
Cái hay ở đây là chỉ dùng có 3 động tác đơn sơ và chỉ trong vài 3 phút mà " Tốn tử" đã biết được số bình chính xác của mình
Truyện bài toán trên là phép chia Euclile ( 1 ) về số học trong tập hợp sô nguyên Z. Vậy ta có thể thay những số 3;5;7;70;21;15;105 trên bằng những nhóm sốkhác như 2;3;5;6;10;30 hay 3;5;11;56;45;165, van vân những theo tôi nhóm số 3;5;7;70;21;15
; 105 trên vẫn đơn giản hơn nhiều
Ví dụ nhóm số : 2;3;5;15;10;6;30
cũng lấu số binh trên 437.
- Nếu xêp 2 người thành một nhóm thì lẻ ra 1 người
- Nếu xếp 3 người vào một nhóm thì lẻ ra 2 người
- nếu xếp 5 người vào một nhóm thì lẻ ra 2 người
và (1x15)+(2x10)+( 2x6)+(3x30) = (15+20+12) + 390 =47 +390 = 437
ở đây 437 phải cộng thêm 3 lần 30, ( ở đây 13x30=390)
(Ý bài nầy là " Tôn Tử " biết chừng chừng số binh của mình. Muốn biết số binh chính xác, thì :
- Làm dấu hiệu thứ nhất - như phất một lần cây cờ - thì cứ 3 người lính đứng lại thành một nhóm, số lính còn lại không lập được một nhóm là 0, 1 hoặc 2 người ; số nầy sẽ nhân với 70.
- Làm dấu hiệu thứ hai, thì cứ 5 người lính đứng lại thành một nhóm, số lính còn lại không lập được một nhóm là 0, 1, 2, 3 hoặc 4 người ; số nầy sẽ nhân cho 21.
- Làm dấu hiệu thứ ba, thì cứ 7 người lính đứng lại thành một nhóm, số lính còn lại không lập được một nhóm là 0, 1, 2, 3, 4, 5 hoặc 6 người ; số nầy sẽ nhân cho 15.
Cọng tất cả 3 số vừa được nhân ở trên, và nếu cần thì cọng thêm, hoặc trừ ra 105, để được số binh chính xác.).
Ví dụ : Số binh là 437, và " Tôn Tử " biết chừng chừng là khoảng 400.
- Nếu sắp 3 người thành một nhóm, thì lẻ ra 2 người,
- Nếu sắp 5 người thành một nhóm, thì lẻ ra 2 người,
- Nếu sắp 7 người thành một nhóm, thì lẻ ra 3 người.
Và : (2 x 70) + (2 x 21) + (3 x 15) + 105 + 105 = (140 + 42 + 45) + 210 = 227 + 210 = 437.
Cái hay ở đây là chỉ dùng có 3 động tác đơn sơ và chỉ trong vài ba phút mà " Tôn Tử " đã biết được số binh chính xác của mình.
Chuyện bài toán trên là Phép Chia Euclide (1) về Số Học trong Tập Hợp Số Nguyên Z. Vậy ta có thể thay những số 3, 5, 7; 70, 21, 15; 105, trên, bằng những nhóm số khác như 2, 3, 5; 15, 10, 6; 30; hay 3, 5, 11; 55, 66, 45; 165 ; vân vân, nhưng theo tôi nhóm số 3, 5, 7; 70, 21, 15; 105 trên vẫn đơn giản hơn nhiều.
Ví dụ với nhóm số 2, 3, 5; 15, 10, 6; 30 :
Cũng lấy số binh trên 437.
- Nếu xếp 2 người thành một nhóm, thì lẻ ra 1 người,
- Nếu xếp 3 người thành một nhóm, thì lẻ ra 2 người,
- Nếu xếp 5 người thành một nhóm, thì lẻ ra 2 người.
Và (1 x 15) + (2 x 10) + (2 x 6) + (13 x 30) = (15 + 20 + 12) + 390 = 47 + 390 = 437.
Ở đây 47 phải cọng thêm 13 lần 30, (13 x 30 = 390).

b)
Gọi số quân là n
n=3x+a => 70n=219x+70a
n=5y+b => 21n=105y+21b
n=7z+c => 15n=105z+15c
Do đó: 106n = 70a +21b + 15c ± 105t (t ∈N)
Vậy n = 70a + 21b + 10c ± 105h (h ∈N)

mình đây
a11.62+(-12).11+50.11
=11.(62+(-12)+50)
=11.(50+50)
11.100=1100
b5/13+-5/7+-20/41+8/13+21/41
=(5/13+8/13)+(-20/41+21/41)+-5/7
=1+1/41+-5/7
=89/287
nhớ tích đúng nha
a, 11.62+(-12).11+50.11
= 11.[62+(-12)+50]
= 11.100 = 1100
b, 5/13 + -5/7 + -20/41 + 8/13 + 21/41
= ( 5/13 + 8/13 ) + [ -20/41 + 21/41 ] + -5/7
= 1 + 1/41 + -5/7
= 89/287

Hay với nhóm số 3, 5, 11; 55, 66, 45; 165 :
Cũng lấy số binh trên 437.
- Nếu xếp 3 người thành một nhóm, thì lẻ ra 2 người,
- Nếu xếp 5 người thành một nhóm, thì lẻ ra 2 người,
- Nếu xếp 11 người thành một nhóm, thì lẻ ra 8 người.
Và (2 x 55) + (2 x 66) + (8 x 45) - 165 = (110 + 132 + 360) - 165 = 602 - 165 = 437.
Ở đây, nếu phải xếp 11 người thành một nhóm, e khó khăn cho binh sĩ nhiều, vì 11 người là một số khá lớn. Cũng vì thế mà nhóm số 3, 5, 7; 70, 21, 15; 105 là đơn giản nhất.
Nếu bài " Điểm Binh của Tôn Tử " đã có từ thời Tôn Tử, khoảng năm 550 trước Công Nguyên, thì trình độ Toán Học của người xua quả đã là cao lắm.
(1) : Theo một số nhà Toán Học hiện đại Euclide (Εὐκλείδη) la? tên một nhóm Toán Học gia ở Alexandrie, vào khoảng năm 300 trước Công Nguyên, cũng như Nicolas Bourbaki là tên của nhóm Toán Học gia nguời Pháp lập tại Besse-et-Saint-Anastaise (Besse-en-Chandesse) vào năm 1935.
Đây chỉ là một vài bài Thơ Toán Dân Gian, tất nhiên còn cả hàng trăm hàng ngàn bài khác. Ngoài ra còn có những người dùng danh từ Toán Học để làm thơ. Trong những bài dưới đây, tôi viết đậm những danh từ Toán Học để nhận thấy rõ ràng.