Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp:
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số
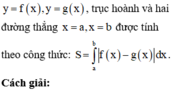
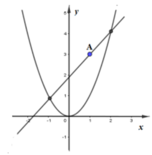

Diện tích hình phẳng giới hạn bởi parabol (P) và đường thẳng d:
S = ∫ x 1 x 2 k x − k + 3 − x 2 d x = 1 2 k x 2 − k − 3 x − 1 3 x 3 x 2 x 1 = 1 2 k x 1 2 − k − 3 x 1 − 1 3 x 1 3 − 1 2 k x 2 2 − k − 3 x 2 − 1 3 x 2 3 = 1 2 k x 1 2 − x 2 2 − k − 3 x 1 − x 2 − 1 3 x 1 3 − x 2 3 = x 1 − x 2 1 2 k x 1 + x 2 − k − 3 − 1 3 x 1 + x 2 2 − x 1 x 2 = x 1 − x 2 1 2 k . k − k − 3 − 1 3 k 2 − k − 3 = x 1 − x 2 1 6 k 2 − 2 3 k + 2
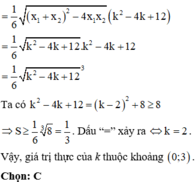

Đáp án B
Phương pháp: Sử dụng công thức ứng dụng tích phân để tính giới hạn của hình phẳng.
Cách giải:
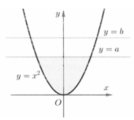
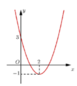
Ta dễ dàng tìm được phương trình parabol là ![]()
Xét phương trình hoành độ giao điểm 
Khi đó diện tích giới hạn bởi (P) và trục hoành là 

Đáp án D
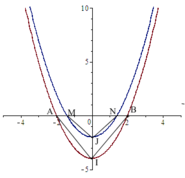
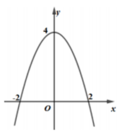
Phép tịnh tiến theo v → 0 ; b biến parabol P : y = x 2 − 4 thành parabol P ' : y = x 2 − 4 + b
Giao điểm của A,B với Ox của (P) có tọa độ lần lượt là: − 2 ; 0 , 2 ; 0
Giao điểm M,N với Ox của (P) có toạn độ lần lượt là: − 4 − b ; 0 , 4 − b ; 0
Đỉnh I,J của parabon (P), (P') có tọa độ lần lượt: 0 ; − 4 , 0 ; − 4 + b
Diện tích tam giác IAB bằng 8 lần diện tích tam giác JMN nên ta có:
I O . A B = 8 J O . M N ⇔ 4.4 = 8. 4 − b .2 4 − b ⇔ 4 − b 3 = 1 ⇔ b = 3 ⇒ J 0 ; − 1


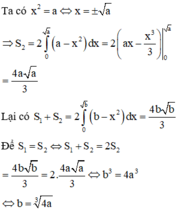


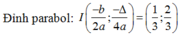


HD: Đường tròn đã cho có phương trình x2 + y2 = 8
Từ đó ta có: y = ±
Gọi S là diện tích phần tô xám ở hình bên :
và
Vậy .
.
c47a4970.html#ixzz43P4gPVRT
Chép y chang cách giải SGK mà chẳng giải thích gì thêm?