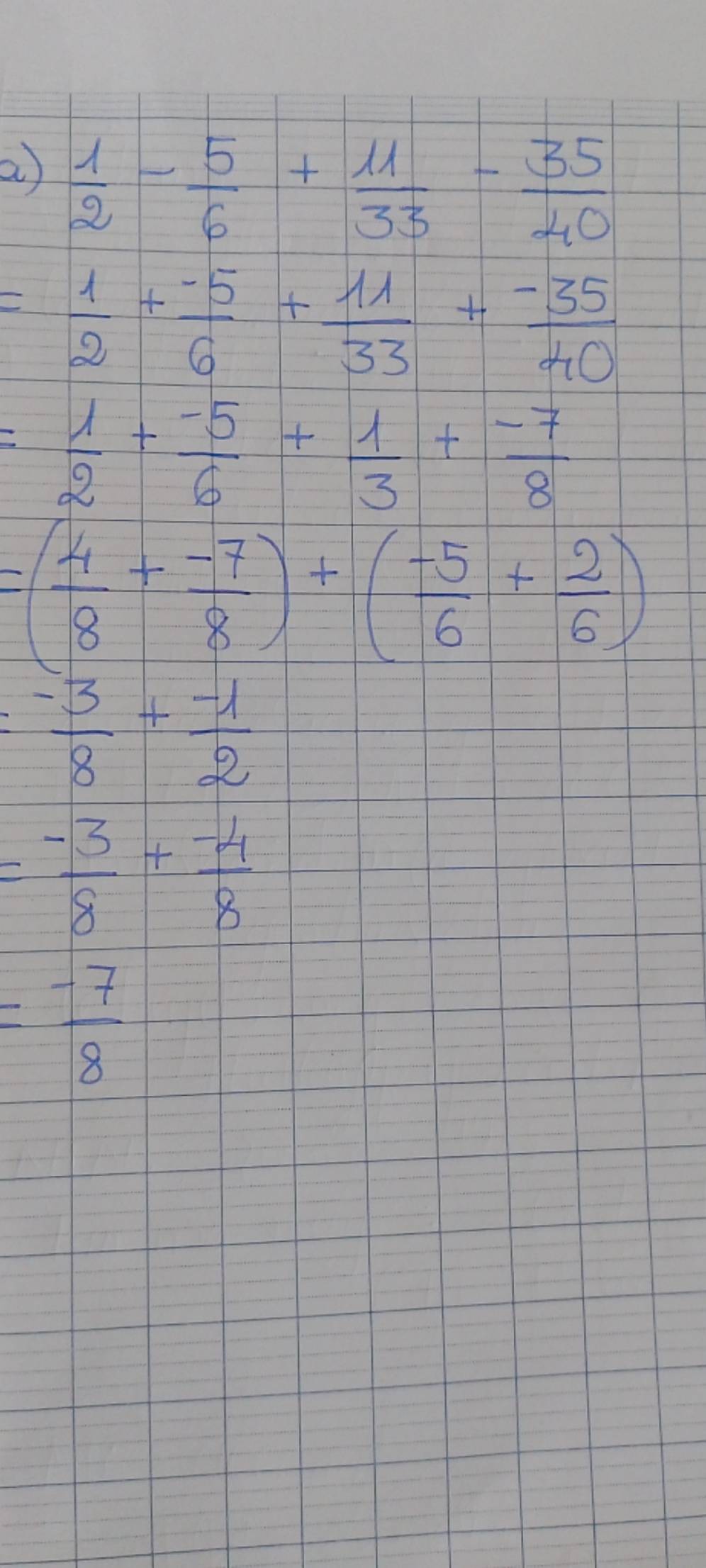Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1: Tính
\(\text{1)}\) \(\dfrac{5}{8}.\dfrac{7}{30}-\dfrac{5}{2}.\dfrac{1}{8}\)
\(=\dfrac{5}{8}.\dfrac{7}{30}-\dfrac{5}{8}.\dfrac{1}{2}\)
\(=\dfrac{5}{8}.\left(\dfrac{7}{30}-\dfrac{1}{2}\right)\)
\(=\dfrac{5}{8}.\dfrac{-4}{15}\)
\(=\dfrac{-1}{6}\)
\(\text{2)}\) \(\dfrac{21}{10}.\dfrac{3}{4}-\dfrac{21}{10}-\dfrac{3}{4}\)
\(=\dfrac{63}{40}-\dfrac{21}{10}-\dfrac{3}{4}\)
\(=\dfrac{-21}{40}-\dfrac{3}{4}\)
\(=\dfrac{-51}{40}\)
\(\text{3)}\) \(\dfrac{-4}{11}:\dfrac{-6}{11}\)
\(=\dfrac{-4}{11}.\dfrac{11}{-6}\)
\(=\dfrac{4}{6}\)
\(\text{4)}\) \(\dfrac{2}{7}.\dfrac{14}{3}-1\)
\(=\dfrac{4}{3}-1\)
\(=\dfrac{1}{3}\)
\(\text{5)}\) \(\dfrac{4}{7}:\left(\dfrac{1}{5}.\dfrac{4}{7}\right)\)
\(=\dfrac{4}{7}:\dfrac{1}{5}:\dfrac{4}{7}\)
\(=1:\dfrac{1}{5}\)
\(=5\)
\(\text{6)}\) \(\dfrac{12}{7}.\dfrac{7}{4}+\dfrac{35}{11}:\dfrac{245}{121}\)
\(=3+\dfrac{35}{11}.\dfrac{121}{245}\)
\(=3+\dfrac{11}{7}\)
\(=3\dfrac{11}{7}=\dfrac{32}{7}\)
\(\text{7)}\) \(\left(\dfrac{4}{3}+\dfrac{8}{3}\right).\left(\dfrac{7}{4}-\dfrac{6}{4}\right):\left(\dfrac{6}{5}+\dfrac{12}{5}+\dfrac{1}{5}\right)\)
\(=4.\left(\dfrac{7}{4}-\dfrac{6}{4}\right):\left(\dfrac{6}{5}+\dfrac{12}{5}+\dfrac{1}{5}\right)\)
\(=4.\dfrac{1}{4}:\left(\dfrac{6}{5}+\dfrac{12}{5}+\dfrac{1}{5}\right)\)
\(=4.\dfrac{1}{4}:\dfrac{19}{5}\)
\(=1:\dfrac{19}{5}\)
\(=\dfrac{5}{19}\)
\(\text{8)}\) \(\left(\dfrac{1}{4}-\dfrac{1}{4}+\dfrac{\dfrac{1}{9}}{\dfrac{1}{9}}\right):\left(\dfrac{2}{3}+\dfrac{\dfrac{7}{15}}{\dfrac{2}{5}}-\dfrac{1}{6}\right)\)
\(=\left(0+1\right):\left(\dfrac{2}{3}+\dfrac{7}{15}:\dfrac{2}{5}-\dfrac{1}{6}\right)\)
\(=1:\left(\dfrac{2}{3}+\dfrac{7}{6}-\dfrac{1}{6}\right)\)
\(=1:\left(\dfrac{2}{3}+1\right)\)
\(=1:\dfrac{5}{3}\)
\(=\dfrac{3}{5}\)
\(\text{9)}\)
\(\left[\left(\dfrac{2}{193}-\dfrac{3}{389}\right).\dfrac{193}{17}+\dfrac{33}{34}\right]:\left[\left(\dfrac{7}{1931}-\dfrac{11}{3862}\right).\dfrac{1931}{25}+\dfrac{9}{2}\right]\)
\(=\left[\dfrac{199}{75077}.\dfrac{193}{17}+\dfrac{33}{34}\right]:\left[\left(\dfrac{7}{1931}-\dfrac{11}{3862}\right).\dfrac{1931}{25}+\dfrac{9}{2}\right]\)
\(=\left[\dfrac{199}{6613}+\dfrac{33}{34}\right]:\left[\left(\dfrac{7}{1931}-\dfrac{11}{3862}\right).\dfrac{1931}{25}+\dfrac{9}{2}\right]\)
\(=\dfrac{13235}{13226}:\left[\left(\dfrac{7}{1931}-\dfrac{11}{3862}\right).\dfrac{1931}{25}+\dfrac{9}{2}\right]\)
\(=\dfrac{13235}{13226}:\left[\dfrac{3}{3862}.\dfrac{1931}{25}+\dfrac{9}{2}\right]\)
\(=\dfrac{13235}{13226}:\left[\dfrac{3}{50}+\dfrac{9}{2}\right]\)
\(=\dfrac{13235}{13226}:\dfrac{114}{25}\)
\(=\dfrac{330875}{1507764}\)

1) \(\frac{5}{8}.\frac{7}{3}-\frac{5}{2}.\frac{1}{8}=\frac{5}{8}.\frac{7}{3}-\frac{5}{8}.\frac{1}{2}=\frac{5}{8}\left(\frac{7}{3}-\frac{1}{2}\right)=\frac{5}{8}.\frac{11}{6}=\frac{55}{48}\)
2) \(\frac{21}{10}.\frac{3}{4}-\frac{21}{10}.\frac{3}{4}=\frac{21}{10}\left(\frac{3}{4}-\frac{3}{4}\right)=\frac{21}{10}.0=0\)
3) \(\frac{-4}{11}:\frac{-6}{11}=\frac{-4}{11}.\frac{-11}{6}=\frac{-4.\left(-11\right)}{11.6}=\frac{-4.\left(-1\right)}{1.6}=\frac{4}{6}=\frac{2}{3}\)
4)\(\frac{2}{7}.\frac{14}{3}-1=\frac{2.14}{7.3}-1=\frac{2.2}{1.3}-1=\frac{4}{3}-1=\frac{1}{3}\)
5)\(\frac{4}{7}:\left(\frac{1}{5}.\frac{4}{7}\right)=\frac{4}{7}:\frac{4}{35}=\frac{4}{7}.\frac{35}{4}=\frac{4.35}{7.4}=\frac{1.5}{1.1}=5\)
6) \(\frac{12}{7}.\frac{7}{4}+\frac{35}{11}:\frac{245}{121}=\frac{12.7}{7.4}+\frac{35}{11}.\frac{121}{245}=\frac{3.1}{1.1}+\frac{35}{11}.\frac{121}{245}=3+\frac{35}{11}.\frac{121}{245}=3+\frac{35.121}{11.245}=\frac{1.11}{1.7}=\frac{11}{7}\)

`@` `\text {Ans}`
`\downarrow`
`a)`
\(\dfrac{1}{2}-\dfrac{5}{6}+\dfrac{11}{33}-\dfrac{35}{40}\)
`=`\(\dfrac{1}{2}-\dfrac{5}{6}+\dfrac{1}{3}-\dfrac{7}{8}\)
`=`\(\dfrac{12}{24}-\dfrac{20}{24}+\dfrac{8}{24}-\dfrac{21}{24}\)
`= -21/24 = -7/8`
`b)`
\(\dfrac{2}{3}\cdot1\dfrac{3}{4}-\dfrac{8}{9}-\dfrac{17}{51}-\dfrac{1}{5}\)
`=`\(\dfrac{2}{3}\cdot\dfrac{7}{4}-\dfrac{8}{9}-\dfrac{17}{51}-\dfrac{1}{5}\)
`=`\(\dfrac{7}{6}-\dfrac{8}{9}-\dfrac{17}{51}-\dfrac{1}{5}\)
`=`\(\dfrac{5}{18}-\dfrac{17}{51}-\dfrac{1}{5}\)
`=`\(-\dfrac{1}{18}-\dfrac{1}{5}=-\dfrac{23}{90}\)
`c)`
\(\dfrac{1}{2}\cdot2-2\dfrac{5}{7}+\dfrac{6}{4}-\dfrac{10}{15}\)
`=`\(1-\dfrac{19}{7}+\dfrac{6}{4}-\dfrac{10}{15}\)
`=`\(-\dfrac{12}{7}+\dfrac{6}{4}-\dfrac{10}{15}\)
`=`\(-\dfrac{3}{14}-\dfrac{10}{15}=-\dfrac{37}{42}\)
`d) `
\(\dfrac{1}{6}\cdot\dfrac{1}{11}+\dfrac{4}{11}\cdot\left(-\dfrac{1}{6}\right)+\dfrac{8}{11}\cdot\dfrac{1}{6}+\dfrac{1}{6}\cdot\dfrac{6}{11}\)
`=`\(\dfrac{1}{6}\cdot\left(\dfrac{1}{11}-\dfrac{4}{11}+\dfrac{8}{11}+\dfrac{6}{11}\right)\)
`=`\(\dfrac{1}{6}\cdot\left(\dfrac{1-4+8+6}{11}\right)\)
`=`\(\dfrac{1}{6}\cdot1=\dfrac{1}{6}\)
`e)`
\(-17\cdot\left(-23\right)+\left(-53\right)\cdot17+17\cdot14+17\cdot\left(-24\right)\)
`= 17*(23-53+14-24)`
`= 17*(-40)`
`= -680`
`f)`
\(-19\cdot218+\left(-82\right)\cdot19-533\cdot19+\left(-19\right)\cdot167\)
`= 19*(-218-82-533-167)`
`= 19*(-1000)`
`= -19000`
`g)`
\(\dfrac{2}{5}+\dfrac{3}{8}-\dfrac{11}{44}+\dfrac{9}{16}\)
`=`\(\dfrac{2}{5}+\dfrac{3}{8}-\dfrac{1}{4}+\dfrac{9}{16}\)
`=`\(\dfrac{31}{40}-\dfrac{1}{4}+\dfrac{9}{16}\)
`=`\(\dfrac{21}{40}+\dfrac{9}{16}=\dfrac{87}{80}\)
`h)`
\(\dfrac{4}{10}-1\dfrac{5}{6}\cdot2+\dfrac{7}{8}-\dfrac{1}{9}\)
`=`\(\dfrac{4}{10}-\dfrac{11}{6}\cdot2+\dfrac{7}{8}-\dfrac{1}{9}\)
`=`\(\dfrac{4}{10}-\dfrac{11}{3}+\dfrac{7}{8}-\dfrac{1}{9}\)
`=`\(-\dfrac{49}{15}+\dfrac{7}{8}-\dfrac{1}{9}\)
`=`\(-\dfrac{287}{120}-\dfrac{1}{9}=-\dfrac{901}{360}\)
`i )`
\(3\cdot\dfrac{1}{5}-\dfrac{2}{8}-\dfrac{12}{36}+\dfrac{15}{9}\)
`=`\(\dfrac{3}{5}-\dfrac{1}{4}-\dfrac{1}{3}+\dfrac{15}{9}\)
`=`\(\dfrac{7}{20}-\dfrac{1}{3}+\dfrac{15}{9}\)
`=`\(\dfrac{1}{60}+\dfrac{15}{9}=-\dfrac{33}{20}\)
`k)`
\(\dfrac{6}{8}\cdot3\dfrac{1}{2}+4\dfrac{2}{3}-\dfrac{11}{55}+\dfrac{17}{51}\)
`=`\(\dfrac{3}{4}\cdot\dfrac{7}{2}+\dfrac{14}{3}-\dfrac{1}{5}+\dfrac{17}{51}\)
`=`\(\dfrac{21}{8}+\dfrac{14}{3}-\dfrac{1}{5}+\dfrac{17}{51}\)
`=`\(\dfrac{175}{24}-\dfrac{1}{5}+\dfrac{17}{51}\)
`=`\(\dfrac{851}{120}+\dfrac{17}{51}=\dfrac{297}{40}\)
`l )`
\(\dfrac{1}{3}\cdot3\dfrac{1}{2}-4\dfrac{2}{5}-\dfrac{26}{78}+\dfrac{17}{51}\)
`=`\(\dfrac{1}{3}\cdot\dfrac{7}{2}-\dfrac{22}{5}-\dfrac{1}{3}+\dfrac{17}{51}\)
`=`\(\dfrac{1}{3}\left(\dfrac{7}{2}-1\right)-\dfrac{22}{5}+\dfrac{17}{51}\)
`=`\(\dfrac{1}{3}\cdot\dfrac{5}{2}-\dfrac{22}{5}+\dfrac{17}{51}\)
`=`\(\dfrac{5}{6}-\dfrac{22}{5}+\dfrac{17}{51}\)
`=`\(-\dfrac{107}{30}+\dfrac{17}{51}=-\dfrac{97}{30}\)
P/s: Bạn tách bài ra hỏi nhé! Và ghi đề rõ ràng chứ đừng ghi ntnay, nhiều bạn nhìn vào rất khó nhìn!
`# \text {KaizulvG}`

a)\(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{9.10}\)
= \(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{3}{4}+...+\frac{1}{9}-\frac{1}{10}\)
= \(1+\left(\frac{-1}{2}+\frac{1}{2}\right)+\left(\frac{-1}{3}+\frac{1}{3}\right)+...+\left(\frac{-1}{9}+\frac{1}{9}\right)-\frac{1}{10}\)
= \(1-\frac{1}{10}\)
=\(\frac{9}{10}\)
b)\(\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+\frac{2}{7.9}+\frac{2}{9.11}\)
= \(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+\frac{1}{7}-\frac{1}{9}+\frac{1}{9}-\frac{1}{11}\)
=\(1+\left(\frac{-1}{3}+\frac{1}{3}\right)+\left(\frac{-1}{5}+\frac{1}{5}\right)+\left(\frac{-1}{7}+\frac{1}{7}\right)+\left(\frac{-1}{9}+\frac{1}{9}\right)-\frac{1}{11}\)
=\(1-\frac{1}{11}\)
= \(\frac{10}{11}\)
c) đặt A=\(\frac{3}{1.3}+\frac{3}{3.5}+\frac{3}{5.7}+\frac{3}{7.9}+\frac{3}{9.11}\)
\(\frac{1}{3}A\)=\(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+\frac{1}{9.11}\)
\(\frac{2}{3}A\)=\(\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+\frac{2}{7.9}+\frac{2}{9.11}\)
\(\frac{2}{3}A\)=\(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+\frac{1}{7}-\frac{1}{9}+\frac{1}{9}-\frac{1}{11}\)
\(\frac{2}{3}A\)=\(1+\left(\frac{-1}{3}+\frac{1}{3}\right)+\left(\frac{-1}{5}+\frac{1}{5}\right)+\left(\frac{-1}{7}+\frac{1}{7}\right)+\left(\frac{-1}{9}+\frac{1}{9}\right)-\frac{1}{11}\)
\(\frac{2}{3}A\)=\(\frac{10}{11}\)
A= \(\frac{10}{11}:\frac{2}{3}\)
A= \(\frac{10}{11}.\frac{3}{2}\)=\(\frac{15}{11}\)
d) giả tương tự câu c kết quả \(\frac{25}{11}\)
tổng đặc biệt đó bạn
\(\frac{1}{1\times2}+\frac{1}{2\times3}+\frac{1}{3\times4}+...+\frac{1}{9\times10}\)
\(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{9}-\frac{1}{10}\)
\(1-\frac{1}{10}=\frac{9}{10}\)
những câu sau cũng áp dụng như vậy nhé

Bài làm
\(A=\left[\left(\frac{2}{193}-\frac{3}{386}\right).\frac{193}{17}+\frac{33}{34}\right]:\left[\left(\frac{7}{2001}+\frac{11}{4002}\right).\frac{2001}{25}+\frac{9}{2}\right]\)
\(=\left[\frac{1}{386}.\frac{193}{17}+\frac{33}{34}\right]:\left[\frac{25}{4002}.\frac{2001}{25}+\frac{9}{2}\right]\)
\(=\left[\frac{1}{34}+\frac{33}{34}\right]:\left[\frac{1}{2}+\frac{9}{2}\right]\)
\(=\frac{1}{5}\)