HK
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
L
2 tháng 11 2019
\((3\sqrt{20}-2\sqrt{80}+\frac{2}{3}\sqrt{45}-\sqrt{5}):\sqrt{5}\)
\(=\left(3\sqrt{2^2.5}-2\sqrt{4^2.5}+\frac{2}{3}\sqrt{3^2.5}-\sqrt{5}\right):\sqrt{5}\)
\(=\left(3.2\sqrt{5}-2.4\sqrt{5}+\frac{2}{3}.3\sqrt{5}\right):\sqrt{5}\)
\(=\left(6\sqrt{5}-8\sqrt{5}+2\sqrt{5}-\sqrt{5}\right):\sqrt{5}\)
\(=-\sqrt{5}:\sqrt{5}=-1\)
L
2 tháng 11 2019
\(\left(\frac{2+\sqrt{5}}{2-\sqrt{5}}-\frac{2-\sqrt{5}}{2+\sqrt{5}}\right).\frac{5-\sqrt{5}}{1-\sqrt{5}}\)
\(=\left(\frac{\left(2+\sqrt{5}\right)^2}{\left(2-\sqrt{5}\right)\left(2+\sqrt{5}\right)}-\frac{\left(2-\sqrt{5}\right)^2}{\left(2-\sqrt{5}\right)\left(2+\sqrt{5}\right)}\right).\frac{\sqrt{5}\left(\sqrt{5}-1\right)}{1-\sqrt{5}}\)
\(=\left(\frac{4+4\sqrt{5}+5-\left(4-4\sqrt{5}+5\right)}{4-5}\right).\frac{-\sqrt{5}\left(1-\sqrt{5}\right)}{1-\sqrt{5}}\)
\(=\frac{9+4\sqrt{5}-9+4\sqrt{5}}{-1}.\left(-\sqrt{5}\right)\)
\(-8\sqrt{5}.\left(-\sqrt{5}\right)=40\)
5 tháng 7 2021
Bài 1 :
a, ĐKXĐ : \(\dfrac{2x+1}{x^2+1}\ge0\)
Mà \(x^2+1\ge1>0\)
\(\Rightarrow2x+1\ge0\)
\(\Rightarrow x\ge-\dfrac{1}{2}\)
Vậy ...
b, Ta có : \(\sqrt[3]{-27}+\sqrt[3]{64}-\sqrt[3]{-\dfrac{128}{2}}\)
\(=-3+4-\left(-4\right)=-3+4+4=5\)
5 tháng 7 2021
Bài 2 :
\(a,=2\sqrt{5}+6\sqrt{5}+5\sqrt{5}-12\sqrt{5}\)
\(=\sqrt{5}\left(2+6+5-12\right)=\sqrt{2}\)
\(b,=\sqrt{5}+\sqrt{5}+\left|\sqrt{5}-2\right|\)
\(=2\sqrt{5}+\sqrt{5}-2=3\sqrt{5}-2\)
\(c,=\dfrac{\left(5+\sqrt{5}\right)^2+\left(5-\sqrt{5}\right)^2}{\left(5-\sqrt{5}\right)\left(5+\sqrt{5}\right)}\)
\(=\dfrac{25+10\sqrt{5}+5+25-10\sqrt{5}+5}{25-5}\)
\(=3\)
LQ
5 tháng 7 2018
1) \(A=\sqrt{x-2013}+\sqrt{2014-x}\)
Biểu thức A có nghĩa khi 2013 < hoặc = x, x < hoặc = 2014
2) \(A=\sqrt{20}+2\sqrt{80}-3\sqrt{45}\\ A=2\sqrt{5}+8\sqrt{5}-9\sqrt{5}\\ A=\sqrt{5}\left(2+8-9\right)\\ A=\sqrt{5}\)
HK
0
KN
30 tháng 7 2019
a)+) \(A=\sqrt{2x^2-3x+1}=\sqrt{2x^2-2x-x+1}\)
\(=\sqrt{2x\left(x-1\right)-\left(x-1\right)}=\sqrt{\left(2x-1\right)\left(x-1\right)}\)
Để A có nghĩa thì \(\hept{\begin{cases}2x-1\ge0\\x-1\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge\frac{1}{2}\\x\ge1\end{cases}}\Leftrightarrow x\ge1\)
hoặc \(\hept{\begin{cases}2x-1\le0\\x-1\le0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\le\frac{1}{2}\\x\le1\end{cases}}\Leftrightarrow x\le\frac{1}{2}\)
A có nghĩa\(\Leftrightarrow\orbr{\begin{cases}x\ge1\\x\le\frac{1}{2}\end{cases}}\)
+) B có nghĩa\(\Leftrightarrow\hept{\begin{cases}x-1\ge0\\2x-1\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge1\\x\ge\frac{1}{2}\end{cases}}\Leftrightarrow x\ge1\)
KN
30 tháng 7 2019
c) \(A=B\Leftrightarrow\sqrt{\left(x-1\right)\left(2x-1\right)}=\sqrt{x-1}.\sqrt{2x-1}\)
\(\Leftrightarrow\hept{\begin{cases}x-1\ge0\\2x-1\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge1\\x\ge\frac{1}{2}\end{cases}}\Leftrightarrow x\ge1\)
Vậy \(x\ge1\)thì A = B
d) \(x\le\frac{1}{2}\)
7 tháng 7 2017
a) A có nghĩa khi (2x+3)/(x-3)>= 0
Trường hợp 1:
2x+3>=0
x>= -3/2(1)
×-3>0
x>3(2)
Từ (1),(2)suy ra x>3
●trường hợp 2
2x+3<= 0
x<=-3/2(3)
x-3<0
x<3(4)
Từ (3),(4) suy ra x<=-3/2
Vậy khi x<=-3/2 hoặc x>3 thì A có nghĩa
B có nghĩa khi (2x+3)/(x_3)>=0
•TH1:
2x+3>=0
x>= -3/2(5)
x-3>0
x>3(6)
Từ (5),(6) suy ra x>3
•TH2:
2x+3<=0
x<=-3/2
Vậy khi x<=-3/2 hoặc x>3 thì B có nghĩa
b) A=B khi x<= -3/2 và x>3
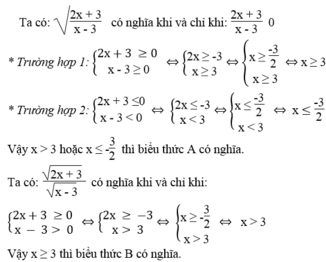
a, \(2\sqrt{5}-3\sqrt{5}+12\sqrt{5}=11\sqrt{5}\)