Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)\(\sqrt{x+1}-\sqrt{x-2}=1\)
Đk:\(x\ge2\)
\(pt\Leftrightarrow\left(\sqrt{x+1}-2\right)-\left(\sqrt{x-2}-1\right)=0\)
\(\Leftrightarrow\dfrac{x+1-4}{\sqrt{x+1}+2}-\dfrac{x-2-1}{\sqrt{x-2}+1}=0\)
\(\Leftrightarrow\dfrac{x-3}{\sqrt{x+1}+2}-\dfrac{x-3}{\sqrt{x-2}+1}=0\)
\(\Leftrightarrow\left(x-3\right)\left(\dfrac{1}{\sqrt{x+1}+2}-\dfrac{1}{\sqrt{x-2}+1}\right)=0\)
Dễ thấy:\(\dfrac{1}{\sqrt{x+1}+2}-\dfrac{1}{\sqrt{x-2}+1}< 0\)
Nên \(x-3=0\Rightarrow x=3\)
b)\(\sqrt{x-1}-\sqrt{5x-1}=\sqrt{3x-2}\)
Đk:\(x\ge1\)
\(pt\Leftrightarrow\sqrt{x-1}=\sqrt{5x-1}+\sqrt{3x-2}\)
\(\Leftrightarrow x-1=5x-1+3x-2+2\sqrt{\left(5x-1\right)\left(3x-2\right)}\)
\(\Leftrightarrow2-7x=2\sqrt{\left(5x-1\right)\left(3x-2\right)}\)
\(\Leftrightarrow49x^2-28x+4=4\left(5x-1\right)\left(3x-2\right)\)
\(\Leftrightarrow49x^2-28x+4=60x^2-52x+8\)
\(\Leftrightarrow-11x^2+24x-4=0\Leftrightarrow\left(2-x\right)\left(11x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{2}{11}\end{matrix}\right.\) (loại hết)
c)\(\sqrt{x}-\sqrt{x+1}-\sqrt{x+4}+\sqrt{x+9}=0\)
Đk:\(x\ge0\)
\(pt\Leftrightarrow\sqrt{x}-\left(\sqrt{x+1}+1\right)-\left(\sqrt{x+4}+2\right)+\left(\sqrt{x+9}-3\right)=0\)
\(\Leftrightarrow\sqrt{x}-\dfrac{x+1-1}{\sqrt{x+1}+1}-\dfrac{x+4-4}{\sqrt{x+4}+2}+\dfrac{x+9-9}{\sqrt{x+9}-3}=0\)
\(\Leftrightarrow\sqrt{x}-\dfrac{x}{\sqrt{x+1}+1}-\dfrac{x}{\sqrt{x+4}+2}+\dfrac{x}{\sqrt{x+9}-3}=0\)
\(\Leftrightarrow x\left(\dfrac{1}{\sqrt{x}}-\dfrac{1}{\sqrt{x+1}+1}-\dfrac{1}{\sqrt{x+4}+2}+\dfrac{1}{\sqrt{x+9}-3}\right)=0\)
Dễ thấy:\(\dfrac{1}{\sqrt{x}}-\dfrac{1}{\sqrt{x+1}+1}-\dfrac{1}{\sqrt{x+4}+2}+\dfrac{1}{\sqrt{x+9}-3}>0\)
Nên \(x=0\)

1) \(\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}=2\) ĐKXĐ \(x\ge1\)
\(\Leftrightarrow\left|\sqrt{x-1}+1\right|+\left|1-\sqrt{x-1}\right|=2\)
ta có:
\(\left|\sqrt{x-1}+1\right|+\left|1-\sqrt{x-1}\right|\)\(\ge\left|\sqrt{x-1}+1+1-\sqrt{x-1}\right|=2\)
dấu "=" xảy ra\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x-1}+1\ge0\\1-\sqrt{x-1}\ge0\end{matrix}\right.\Leftrightarrow x\le2\)
kết hợp vs điều kiện ta có nghiệm của phương trình \(\left\{x|1\le x\le2\right\}\)
câu 2,4 tương tự
3) \(\sqrt{x-2-2\sqrt{x-3}}=1\)

Câu 1:
\(A=\sqrt{2-\sqrt{3}}-\dfrac{1}{\sqrt{2-\sqrt{3}}}\)
\(=\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\)
\(=\dfrac{\sqrt{4-2\sqrt{3}}-\sqrt{4+2\sqrt{3}}}{\sqrt{2}}\)
\(=\dfrac{\sqrt{3}-1-\sqrt{3}-1}{\sqrt{2}}=-\sqrt{2}\)

\(a.\left(2-\sqrt{3}+\sqrt{5}\right)\left(2-\sqrt{5}+\sqrt{3}\right)\)
\(=4-\left(\sqrt{3}-\sqrt{5}\right)^2\)
\(=4-3+2\sqrt{15}-5\)
\(=2\sqrt{15}-4\)
\(b.2\sqrt{3}\left(\sqrt{3}-3\right)-\left(3\sqrt{3}-1\right)^2\)
\(=6-6\sqrt{3}-27+6\sqrt{3}-1\)
\(=-22\)
![]()

a/ \(\sqrt{8-2\sqrt{15}}-\sqrt{8+2\sqrt{15}}=\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}-\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}\) \(=\sqrt{5}-\sqrt{3}-\sqrt{5}-\sqrt{3}=-2\sqrt{3}\).
b/ \(A=\sqrt{4+\sqrt{10+2\sqrt{5}}}+\sqrt{4-\sqrt{10+2\sqrt{5}}}\Rightarrow A^2=8+2\sqrt{4^2-\left(\sqrt{10+2\sqrt{5}}\right)^2}=8+2\sqrt{6-2\sqrt{5}}\) \(=8+2\sqrt{\left(\sqrt{5}-1\right)^2}=8+2\sqrt{5}-2=6+2\sqrt{5}=\left(\sqrt{5}+1\right)^2\)
\(\Rightarrow A=\sqrt{5}+1\)
c/ \(B=\sqrt{4+\sqrt{15}}+\sqrt{4-\sqrt{15}}-2\sqrt{3-\sqrt{5}}\Rightarrow\sqrt{2}B=\sqrt{8+2\sqrt{15}}+\sqrt{8-2\sqrt{15}}-2\sqrt{6-2\sqrt{5}}=\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}+\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}-2\sqrt{\left(\sqrt{5}-1\right)^2}=\sqrt{5}+\sqrt{3}+\sqrt{5}-\sqrt{3}-2\sqrt{5}+2=2\Rightarrow B=\sqrt{2}\)

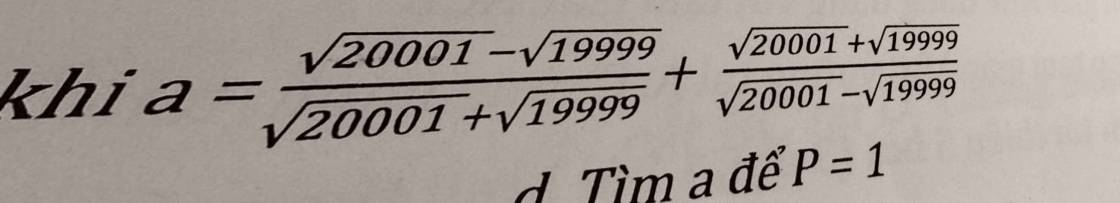
 Giải thích dùm mình sao
Giải thích dùm mình sao
Đặt \(\sqrt{20001}=a;\sqrt{19999}=b\)
\(A=\dfrac{a-b}{a+b}+\dfrac{a+b}{a-b}\)
\(=\dfrac{\left(a-b\right)^2+\left(a+b\right)^2}{\left(a+b\right)\left(a-b\right)}=\dfrac{2\left(a^2+b^2\right)}{a^2-b^2}\)
\(=\dfrac{2\left(20001+19999\right)}{20001-19999}=40000\)