
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ở đây chỉ thấy các câu 26, 32, 34, 36
26.
\(S_{ABC}=\dfrac{1}{2}AB^2=\dfrac{a^2}{18}\)
\(BC=AB\sqrt{2}=\dfrac{a\sqrt{2}}{3}\Rightarrow p=\dfrac{AB+AC+BC}{2}=\dfrac{2a+a\sqrt{2}}{6}\)
\(\Rightarrow r=\dfrac{S}{p}=\dfrac{6a^2}{18a\left(2+\sqrt{2}\right)}=\dfrac{\left(2-\sqrt{2}\right)a}{6}\)
32.
Đường thẳng nhận \(\overrightarrow{n}=\left(5;-1\right)\) là 1 vtpt
34.
Áp dụng định lý hàm cos:
\(c=\sqrt{a^2+b^2-2ab.cosC}=\sqrt{8^2+7^2-2.8.7.cos60^0}=\sqrt{57}\)
36.
\(y=\sqrt{\dfrac{x^2-2mx+5m}{2021}}\)
Hàm xác định trên R khi và chỉ khi: \(x^2-2mx+5m\ge0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=m^2-5m\le0\Rightarrow0\le m\le5\)
Có 5 giá trị nguyên dương của m thỏa mãn (1;2;3;4;5)

Thời gian hai xe gặp nhau là:
24:(48-32)=3/2 giờ=1 giờ 30 phút
Lúc đó là:
6h45'+1h30'=8h15'


Đặt \(p=x+y+z\)
\(q=xy+zy+zx\)
\(r=xyz\)
Ta có :
\(2q=\left(x+y+z\right)^2-\left(x^2+y^2+z^2\right)=4-6=-2\Rightarrow q=-1\)
Bây giờ ta sẽ đi tìm r
Đặt \(S_n=x^n+y^n+z^n\)
Khi đó \(S_0=3\)
\(S_1=-2\)
\(S_2=6\)
Ta có :
\(S_n-\left(x+y+z\right)S_{n-1}+\left(xy+yz+zx\right)S_{n-2}-xýzS_{n-3}=0\)
Suy ra \(S_n=-2S_{n-1}+S_{n-2}+rS_{n-3}\)
Lấy n = 3, ta được :
\(S_3=-2S_2+S_1+rS_0=-14+3r\)
Lấy n = 4, ta được :
\(S_4=-2S_3+S_2+rS_1=28-6r+6-2r=34-8r\)
Lấy n = 5, ta được :
\(S_5=-2S_4+S_3+rS_2=-68+16r-14+3r+6r=-82+25r\)
Mà \(S_5=-32\) nên r = 2.
Do đó x, y, z là nghiệm của phương trình
\(t^3+2t^2-t-2=0\Leftrightarrow t\in\left\{1;-1;-2\right\}\)
Vậy nghiệm của hệ là \(\left\{1;-1;-2\right\}\) và các hoán vị của nó

ta có : 2020 \(⋮\)4 nên năm 2020 là năm nhuận và có 366 ngày
Mà 25 là thứ 2 nên cứ sau 1 tuần ( 7 ngày ) thì lại có 1 ngày thứ 2
có : 366 : 7=52 dư 2
vậy sau 366 ngày là \(\approx\) 52 tuần và 2 ngày là thứ 2+2=4
Vậy ngày 25 tháng 5 năm 2021 là thứ 4
Vì năm 2021 là năm không nhuận nên có 365 ngày.
Ta co: 365 : 7 = 52( dư 1)
Ta thêm 1 ngày vào thứ 2 thì ra thứ 3.


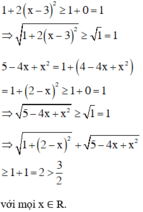
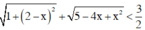 vô nghiệm.
vô nghiệm.
TL : 6,4
32:5=32:5 bn nhéฅ^•ﻌ•^ฅ