Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C M I H
a) Theo đề bài ta có :
\(MI//CA\) ( GT)
=> ACMI là hình thang ( định nghĩa)
Xét hình thang ACMI ta có :
\(\widehat{A}=90^o\)
=> ACMI là hình thang vuông

a, Vì AC // MI
=> Tứ giác ACMI là hình thang
Vì góc A=90 độ
=> Tứ giác ACMI là hình thang vuông

a: Xét tứ giác ACMI có MI//AC và góc CAI=90 độ
nen ACMI là hình thang vuông
b: Ta có; góc HAM+góc CMA=90 độ
góc IAM+góc CAM=90 độ
mà góc CMA=góc CAM
nên góc HAM=góc IAM
=>AM là phân giác của góc IAH
Xét ΔAIM vuông tại I và ΔAHM vuông tại H có
AM chung
góc IAM=góc HAM
Do đo: ΔAIM=ΔAHM
Suy ra: AI=AH
c: \(\left(AB+AC\right)^2=AB^2+AC^2+2\cdot AB\cdot AC=BC^2+2\cdot AH\cdot BC\)
\(\left(AH+BC\right)^2=AH^2+2\cdot AH\cdot BC+BC^2>2\cdot AH\cdot BC+BC^2\)
=>AH+BC>AB+AC

Đáp án cần chọn là: C
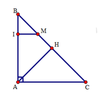
Tứ giác ACMI có: MI //AC (gt) và A ^ = 90 ° (gt) nên là hình thang vuông.

a) Tự cm
b) Vì AB//DM mà ABvuoong góc với AC nên DM vuông góc với AC
Vì AH vuông góc với BC mà M thuộc BC nên CH vuông góc với AD
Xét tam giác ADC có:
DM vuông góc với AC
CM vuông góc với AD
mà DM cắt CM tại M
=> M là trực tâm của tam giác ADC
=> AM vuông góc với CD
=> đpcm
c) Xét tam giác NCm có
I là trung điểm của CM
=> IM=IN=IC
Xét tam giác IN< có
IM=IN
=> IMN cân tại I
=> IMN=INM góc
mà IMN=DMH
=> INM=DMH(3)
Xét tam giác AND có
H là trung điểm của AD
=> NH=HD=HA
tương tự tam giác NHD cân tại H
=>D=N( góc)(2)
mà HDN+DMH=90 độ(1)
Từ 1.2.3=> INM+MNH=90 độ
hay IN vuông góc với NH
đpcm

a: Xét tứ giác ACMI có MI//AC
nên ACMI là hình thang
mà góc CAI=90 độ
nên ACMI là hình thang vuông
b: Ta có: góc BAM+góc CAM=90 độ
góc HAM+góc CMA=90 độ
mà góc CAM=góc CMA
nên góc BAM=góc HAM
=>AM là phân giác của góc BAH
Xét ΔAIM vuông tại I và ΔAHM vuông tại H có
AM chung
góc HAM=góc IAM
DO đó: ΔAIM=ΔAHM
Suy ra: AI=AH
c: \(\left(AB+AC\right)^2-\left(AH+BC\right)^2\)
\(=AB^2+AC^2+2AB\cdot AC-AH^2-BC^2-2\cdot AH\cdot BC\)
\(=-AH^2< 0\)
=>AB+AC<AH+BC