
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


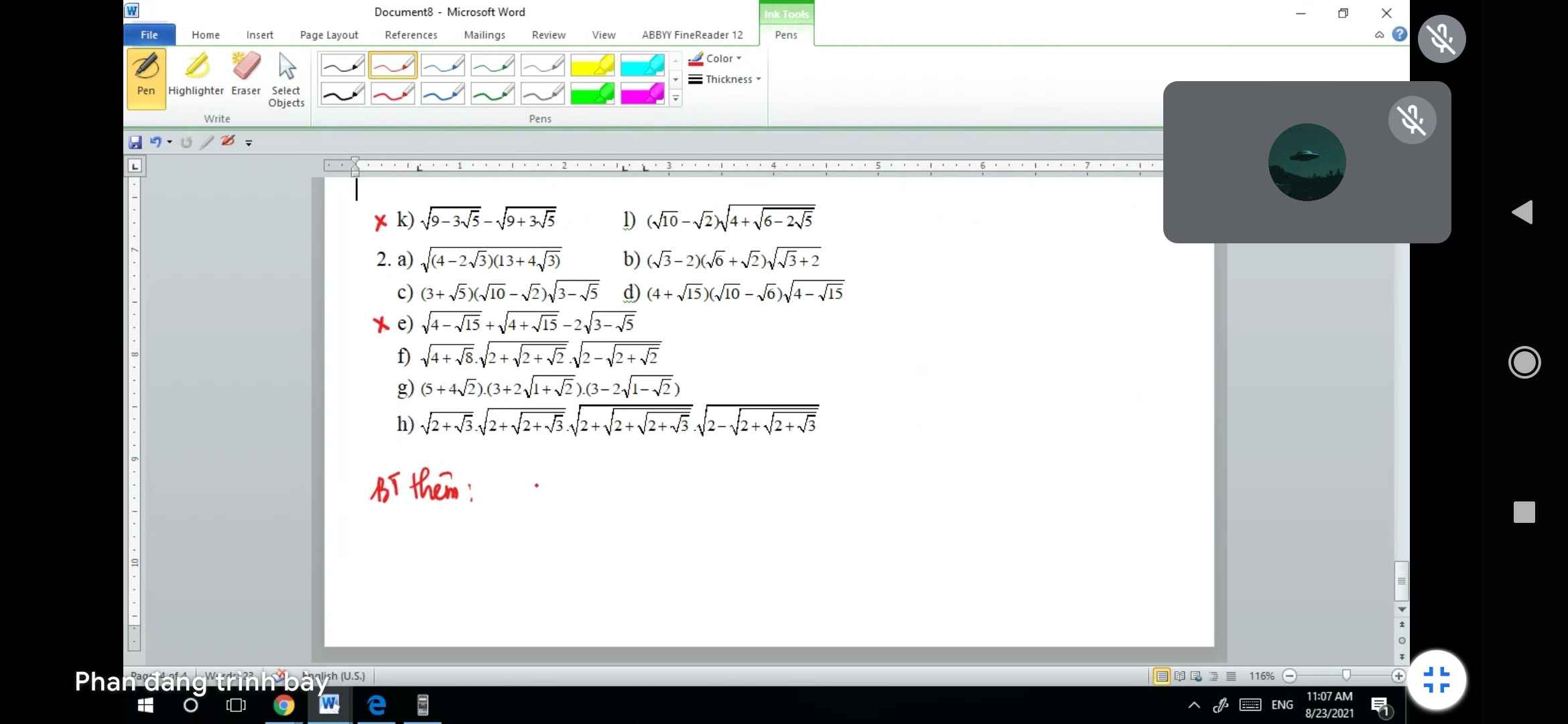
\(\sqrt{9-3\sqrt{5}}-\sqrt{9+3\sqrt{5}}=\dfrac{1}{\sqrt{2}}\left(\sqrt{18-6\sqrt{5}}-\sqrt{18+6\sqrt{5}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{15}-\sqrt{3}\right)^2}-\sqrt{\left(\sqrt{15}+\sqrt{3}\right)^2}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{15}-\sqrt{3}-\sqrt{15}-\sqrt{3}\right)=-\dfrac{2\sqrt{3}}{\sqrt{2}}=-\sqrt{6}\)
\(\sqrt{4-\sqrt{15}}+\sqrt{4+\sqrt{15}}-2\sqrt{3-\sqrt{5}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{8-2\sqrt{15}}+\sqrt{8+2\sqrt{15}}-2\sqrt{6-2\sqrt{5}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}+\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}-2\sqrt{\left(\sqrt{5}-1\right)^2}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{5}-\sqrt{3}+\sqrt{5}+\sqrt{3}-2\left(\sqrt{5}-1\right)\right)\)
\(=\dfrac{2}{\sqrt{2}}=\sqrt{2}\)
k: Ta có: \(\sqrt{9-3\sqrt{5}}-\sqrt{9+3\sqrt{5}}\)
\(=\dfrac{\sqrt{18-6\sqrt{5}}-\sqrt{18+6\sqrt{5}}}{\sqrt{2}}\)
\(=\dfrac{\sqrt{15}-\sqrt{3}-\sqrt{15}-\sqrt{3}}{\sqrt{2}}\)
\(=-\sqrt{6}\)


Bài 5:
\(\sqrt{x-7}+\sqrt{9-x}=x^2-16x+66\) (*) (đk \(7\le x\le9\))
Vs a,b >0 có:\(\sqrt{a}+\sqrt{b}\le2\sqrt{\frac{a+b}{2}}\)(tự CM nha)
Dấu "=" xảy ra <=> a=b
Áp dụng bđt trên có:
\(\sqrt{x-7}+\sqrt{9-x}\le2\sqrt{\frac{x-7+9-x}{2}}=2\sqrt{1}=2\)(1)
Có x2-16x+66=(x2-16x+64)+2=(x-8)2+2\(\ge2\)
=> x2-16x+66 \(\ge2\) (2)
Từ (1),(2).Dấu "=" xảy ra<=> \(\left\{{}\begin{matrix}x-7=9-x\\x-8=0\end{matrix}\right.\)<=>\(\left\{{}\begin{matrix}2x=16\\x=8\end{matrix}\right.\)<=>\(\left\{{}\begin{matrix}x=8\\x=8\end{matrix}\right.\)<=> x=8( tm pt (*))
Vậy pt (*) có nghiệm x=8




Giá xe cũ trước khi giảm giá lần 2 là:
684000000:90%=760000000(đồng)
Giá xe cũ trước khi giảm giá lần 1 là:
760000000:95%=800000000(đồng)
Giá xe mới là:
800000000*125%=1000000000(đồng)




1234583 + 987736489 = 988971072
988971072 bạn nhé