Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) - x + 2 + 2(y - 2) < 2(1 - x) <=> y <
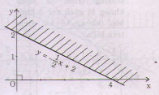
Tập nghiệm của bất phương trình là:
T = {(x, y)|x ∈ R; y < }.
Để biểu diễn tập nghiệm T trên mặt phẳng tọa độ, ta thực hiện:
+ Vẽ đường thẳng (d): y=
+ Lấy điểm gốc tọa độ O(0; 0) (d).
Ta thấy: 0 < - 0 + 2. Chứng tỏ (0; 0) là một nghiệm của bất phương trình. Vậy nửa mặt phẳng bờ là đường thẳng (d) (không kể bờ) chứa gốc O(0; 0) là tập hợp các điểm biểu diễn tập nghiệm của bất phương trình đã cho (nửa mặt phẳng không bị gạch sọc)

Thay \(x=-3\) vào bất phương trình (1) ta được:
\(3.\left(-3\right)+1< -3+3\)\(\Leftrightarrow-8< 0\) ( đúng)
Vậy \(x=-3\) là nghiệm của bất phương trình (1)
TThay \(x=-3\) vào bất phương trình (2) ta được:
\(\left(3.\left(-3\right)+1\right)^2< \left(-3+3\right)^2\)\(\Leftrightarrow64< 0\) (vô lý).
Vậy \(x=-3\) là nghiệm của bất phương trình (2).
Vậy hai bất phương trình (1) và (2) không tương đương và bình phương hai vế của bất phương trình không là phép biến đổi tương đương.

a) \(x^2\ge4x\)(1)
Nếu \(\left[{}\begin{matrix}x_1=0\\x_2=4\end{matrix}\right.\) \(\Rightarrow VT=VP\)
Nếu \(x< 0\Rightarrow VT>0;VP< 0\)=> \(VT>VP\)
Nếu 0<x<4 \(\Rightarrow VT< VP\)
nếu x> 4\(\Rightarrow VT>VP\)
Kết luận nghiệm BPT (1): \(\left[{}\begin{matrix}x\le0\\x\ge4\end{matrix}\right.\)
b)
(1) \(\Rightarrow\left[{}\begin{matrix}x< \dfrac{3-\sqrt{5}}{2}\\x>\dfrac{3+\sqrt{5}}{2}\end{matrix}\right.\)
(2) \(\Rightarrow-2\le x\le3\)
KL nghiệm
\(\left[{}\begin{matrix}-2\le x< \dfrac{3-\sqrt{5}}{2}\\\dfrac{3+\sqrt{5}}{2}< x\le3\end{matrix}\right.\)
a)\(Bpt\Leftrightarrow\) \(\left\{{}\begin{matrix}x^2-4x\ge0\left(1\right)\\\left(2x-1\right)^2-9>0\left(2\right)\end{matrix}\right.\)
Giải (1): \(x^2-4x\ge0\Leftrightarrow\left[{}\begin{matrix}x\ge4\\x\le0\end{matrix}\right.\)
Giải (2): \(\left(2x-1\right)^2-9=\left(2x-1\right)^2-3^2=\left(2x-4\right)\left(2x+2\right)\)
\(\left(2x-4\right)\left(2x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Vì vậy: \(\left(2x-1\right)^2-9< 0\Leftrightarrow-1< x< 2\).
Kết hợp điều kiện \(\left(1\right)\) và \(\left(2\right)\) suy ra: \(-1< x\le0\) thỏa mãn hệ bất phương trình.

Điều kiện xác định :\(x\ne-1\)
Ta có : \(\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)=1\Rightarrow\left(2-\sqrt{3}\right)=\left(2+\sqrt{3}\right)^{-1}\)
\(\Rightarrow\) Bất phương trình : \(\left(2+\sqrt{3}\right)^{x-1}\ge\left(2+\sqrt{3}\right)^{\frac{1-x}{x+1}}\)
\(\Leftrightarrow x-1\ge\frac{1-x}{x+1}\)
\(\Leftrightarrow\frac{\left(x-1\right)\left(x+2\right)}{x+1}\ge0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}-2\le x< -1\\x\ge1\end{array}\right.\)
Vậy bất phương trình có tập nghiệm là \(S=\)[ -2; -1) \(\cup\) [1; \(+\infty\))
1 ) \(|\) x+2 \(|\) - \(|\) x-1 \(|\) < x - 3/2
TH1 : x < -2
bpt <=> -x - 2 - ( -x + 1) < x - 3/2
<=> x > -3/2 ( k tm )
TH 2 : -2 \(\le\) x < 1
bpt <=> x + 2 - ( -x+1) < x - 3/2
<=> x < -5/2 (k tm )
TH3 : x \(\ge\) 1
bpt <=> x + 2 - ( x - 1 ) < x - 3/2
<=> x > 9/2 tm
Vậy x > 9/2 .
2 ) x(x - 1)2 \(\ge\) 4 - x
<=> x( x2 - 2x +1 + 1 ) \(\ge\) 4
<=> x3 - 2x2 + 2x - 4 \(\ge\) 0
<=> x2 (x - 2) + 2(x - 2) \(\ge\) 0
<=> (x2 + 2)(x - 2) \(\ge\) 0
Có : x2 + 2 > 0 , với mọi x
=> x - 2 \(\ge\) 0 <=> x \(\ge\) 2 .
Xem thử đúng hay sai ...
Hoàng Thị Ánh Phương , Ribi Nkok Ngok, Nguyễn Lê Phước Thịnh, Trần Quốc Khanh, Vũ Minh Tuấn, ?Amanda?, Nguyễn Ngọc Lộc , Trên con đường thành công không có dấu chân của kẻ lười biếng, Bùi Lan Anh , Akai Haruma, @Nguyễn Việt Lâm, ...