Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. xét tam giác OBK và tam giác IBK có : BK chung
góc OBK = góc IBK do BK là pg của góc OBM (gt)
OB = BI (gt)
=> tam giác OBK = tam giác IBK (c-g-c)
b, tam giác OBK = tam giác IBK (câu a)
=> góc KOB = góc KIB (đn)
có góc KOB = 90
=> góc KIB = 90
=> KI _|_ BM (đn)
c, xét tam giác KOA và tam giác KIM có : góc AKO = góc MKI (đối đỉnh)
KO = KI do tam giác OBK = tam giác IBK (câu a)
góc KOA = góc KIM = 90
=> tam giác KOA = tam giác KIM (cgv-gnk)
=> AK = KM (Đn)

a) xét tam giác OBK và tam giác IBK có:
KB là cạnh chung
góc OBK= góc KBI (do BI là tia phân giác của góc B)
OB=IB (gt)
suy ra :tam giác OBK = tam giác KBI(1)
b) từ (1) suy ra góc KOB = góc KIB=900( 2 góc tương ứng ) (2)
c) xét tam giác OAK và tam giác IMK có:
góc AKO= góc IKM ( đối đỉnh)
góc AOK= góc KIM
OK=KI ( 2 góc tươg ứng chứng mih ở câu a)
suy ra tam giác OAK= tam giác IMK
suy ra AK=KM (2 cạnh tương ứng )
c)

a) Xét tam giác ADB và AEC có:
AD = AE (gt)
AB = AC (gt)
Góc A chung
\(\Rightarrow\Delta ADB=\Delta AEC\left(c-g-c\right)\Rightarrow BD=CE\)
b) Do AB = AC; AD = AE nên BE = DC
Xét tam giác CEB và BDC có:
CE = BD (cma)
Cạnh BC chung
BC = CD (cmt)
\(\Rightarrow\Delta CEB=\Delta BDC\left(c-c-c\right)\)
c) Do \(\Delta ADB=\Delta AEC\Rightarrow\widehat{EBI}=\widehat{DCI}\)
Do \(\Delta CEB=\Delta BDC\Rightarrow\widehat{BEI}=\widehat{CDI}\)
Xét tam giác BIE và tam giác CID có:
\(\widehat{EBI}=\widehat{DCI}\)
\(\widehat{BEI}=\widehat{CDI}\)
BE = CD
\(\Rightarrow\Delta BIE=\Delta CID\left(g-c-g\right)\)
d) Do \(\Delta BIE=\Delta CID\Rightarrow IB=IC\)
Lại có AB = AC nên IA là trung trực của BC
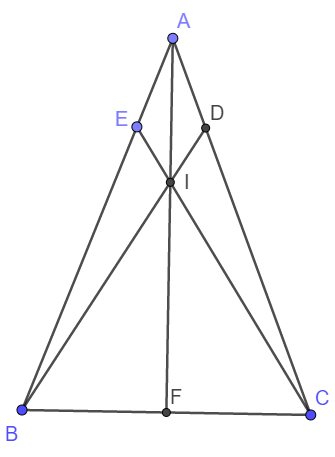
Vậy IA đi qua trung điểm F của BC hay A, I, F thẳng hàng.

Em tham khảo tại đây nhé.
Câu hỏi của Phạm Bá Gia Nhất - Toán lớp 7 - Học toán với OnlineMath

Bài này easy lắm bạn
B A C D E F I Hình ảnh chỉ mang tính chất minh họa
a) Xét \(\Delta\) ABD và \(\Delta\)ACE có
AB = AC ( gt)
\(\widehat{BAC}\) : góc chung
AD = AE ( gt)
=> \(\Delta\)ABD = \(\Delta\) ACE (c-g-c)
=> BD = CE ( 2 cạnh tương ứng )
+) Ta có \(\hept{\begin{cases}AB=AC\left(gt\right)\\AE=AD\left(cmt\right)\end{cases}}\)
\(\Rightarrow AB-AE=AC-AD\)
\(\Rightarrow\)BE = CD
+) Xét \(\Delta\)CEB và \(\Delta\)BDC có
CE = BD ( cmt)
EB = DC ( cmt)
CB: cạnh chung
=> \(\Delta\)CEB = \(\Delta\) BDC (c-c-c)
2 câu này đã nhé

Em tham khảo tại đây nhé.
Câu hỏi của Phạm Bá Gia Nhất - Toán lớp 7 - Học toán với OnlineMath

Hình tự vẽ nak !
a, Xét tam giác OBK và tam giác IBK có:
^B1 = ^B2 (Phân giác)
BO = BI (gt)
BK chung
=> Tam giác OBK = tam giác IBK (c.g.c)
b, Vì Tam giác OBK = tam giác IBK (cmt)
=> ^KIB = ^KOB = 90o
=> KI vuông góc BM
c, Vì Tam giác OBK = tam giác IBK
=> KI = KO
Xét tam giác KOA và tam giác KIM có
^K1 = ^K2 (đối đỉnh)
KI = KO (cmt)
^KOA = ^KIM (=90o)
=> tam giác KOA = tam giác KIM(g.c.g)
=> KA = KM
Vậy .......
O B M K I A 1 2 1 2
a, Xét tam giác OBK và tam giác IBK có:
^B1 = ^B2 (Phân giác)
BO = BI (gt)
BK chung
=> Tam giác OBK = tam giác IBK (c.g.c)
b, Vì Tam giác OBK = tam giác IBK (cmt)
=> ^KIB = ^KOB = 90o
=> KI vuông góc BM
c, Vì Tam giác OBK = tam giác IBK
=> KI = KO
Xét tam giác KOA và tam giác KIM có
^K1 = ^K2 (đối đỉnh)
KI = KO (cmt)
^KOA = ^KIM (=90o)
=> tam giác KOA = tam giác KIM(g.c.g)
=> KA = KM
Vậy .......

4:
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF
c: AE=AF
ME=MF
=>AM là trung trực của EF
mà K nằm trên trung trực của EF
nên A,M,K thẳng hàng