Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình bạn tự vẽ nha
| GT | ΔACB vuông tại A, BD là phân giác, AB/CB=3/5; AC=16cm |
| KL | a: AB=?; BC=? b: AD=?; CD=? |
a: AB/BC=3/5
=>AB/3=BC/5=k
=>AB=3k; BC=5k
BC^2=AB^2+AC^2
=>16k^2=16^2=256
=>k^2=16
=>k=4
=>AB=12cm; CB=20cm
b: BD là phân giác
=>AD/AB=CD/BC
=>AD/3=CD/5=(AD+CD)/(3+5)=16/8=2
=>AD=6cm; CD=10cm

a: AB/BC=3/5
=>AB/3=BC/5=k
=>AB=3k; BC=5k
BC^2=AB^2+AC^2
=>16k^2=16^2=256
=>k^2=16
=>k=4
=>AB=12cm; CB=20cm
b: BD là phân giác
=>AD/AB=CD/BC
=>AD/3=CD/5=(AD+CD)/(3+5)=16/8=2
=>AD=6cm; CD=10cm

a) Vì tam giác ABC vuông tại A
=> BAC = 90 độ
=> Vì K là hình chiếu của H trên AB
=> HK vuông góc với AB
=> HKA = 90 độ
=> HKA = BAC = 90 độ
=> KH // AI
=> KHIA là hình thang
Mà I là hình chiếu của H trên AC
=> HIA = 90 độ
=> HIA = BAC = 90 độ
=> KHIA là hình thang cân
b) Vì KHIA là hình thang cân
=> KA = HI
= >KI = HA
Xét tam giác KAI vuông tại A và tam giác HIC vuông tại I có
KA = HI
KI = AH
=> Tam giác KAI = tam giác HIC ( cgv-ch)
=> KIA = ACB ( DPCM)
c) con ý này tớ nội dung chưa học đến thông cảm

A B C D E 1 2 1
Qua B kẻ đường thẳng song song cới AD và cắt tia CA tại E.
Ta có: ^A1=^B1 (So le trong); ^A2=^E (Đồng vị). Mà ^A1=^A2 => ^B1=^E
=> \(\Delta\)BAE cân tại A => AE=AB=2
Sử dụng định lí Ta-lét: \(\frac{AD}{EB}=\frac{AC}{EC}\Rightarrow\frac{1,2}{EB}=\frac{3}{AC+AE}\Rightarrow\frac{1,2}{EB}=\frac{3}{3+2}\Rightarrow\frac{1,2}{EB}=\frac{3}{5}\)
\(\Rightarrow EB=1,2:\frac{2}{5}=\frac{1,2.5}{3}=\frac{6}{3}=2\)\(\Rightarrow AE=AB=EB=2\)
\(\Rightarrow\Delta\)BAE đều \(\Rightarrow\widehat{BAE}=60^0\). Mà ^BAE kề bù với ^BAC
\(\Rightarrow\widehat{BAC}=120^0\).

\(AC=\sqrt{20^2-12^2}=16\left(cm\right)\)
Xét ΔACB có AD là phân giác
nên DB/AB=DC/AC
=>DB/3=DC/4=(DB+DC)/(3+4)=20/7
=>DB=60/7cm; DC=80/7cm

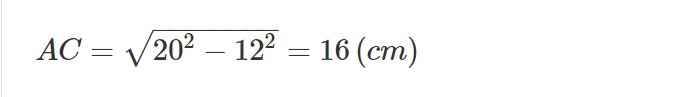
Xét ΔACB có AD là phân giác
nên DB/AB=DC/AC
=>DB/3=DC/4=(DB+DC)/(3+4)=20/7
=>DB=60/7cm; DC=80/7cm

a. Xét tam giác HCD cóHN=DN;HM=CM
=> MN là đường trung bình của tam giác HCD => MN//DC
=> DNMC là hình thang
b. Ta có MN là đường trung bình của tam giác HCD => MN=1/2CD
Mà AB=1/2CD => AB =MN
Do MN//CD và AB//CD => AB//MN
Xét tứ giác ABMN có AB//MN; AB=MN
=> ABMN là hình bình hành
c.Ta có MN//CD mà CD vg AD
=> MN vg AD
Xét tam giác ADM có DH và MN là 2 đường cao của tam giác
Mà chúng cắt nhau tại N nên N là trực tâm của tam giác ADM
=> AN là đường cao của tam giác ADM
=> AN vg DM
Do ABMN là hình bình hành nên AN//BM
=> BM vg DM => BMD =90*
A B C 16 D
Với `(AB)/(BC) = 3/5`
`=> (AB)/3 = (BC)/5`
Đặt `(AB)/3 = (BC)/5 = k (k > 0)`
`=> AB = 3k; BC = 5k`
Áp dụng định lý pitago vào tam giác `ABC` vuông tại `A`
`=> AB^2 + AC^2 = BC^2`
`=> (3k)^2 + 16^2 = (5k)^2`
`=> 9k^2 + 256 = 25k^2`
`=> 16k^2 = 256`
`=> k^2 = 16`
`=> k^2 = 4^2`
`=> k = 4 (`Vì `k > 0)`
Khi đó: `AB = 3k = 4 . 3 = 12 (cm)`
`BC = 5k = 5 . 4 = 20 (cm)`
b) Tam giác `ABC` có BD là tia phân giác của tam giác `ABC`. Áp dụng tính chất đường phân giác trong tam giác
`=> (AD)/(AB) = (DC)/(BC) `
`=> (AD)/12 = (DC)/20`
Áp dụng tính chất dãy tỉ số bằng nhau
`=> (AD)/12 = (DC)/20 = (AD + DC)/(12 + 20) = 16/32 = 1/2`
`=> AD = 1/2 xx 12 = 6 (cm) ; DC = 1/2 xx 20 = 10 (cm)`
a: AB/BC=3/5
=>AB/3=BC/5=k
=>AB=3k; BC=5k
BC^2=AB^2+AC^2
=>16k^2=16^2=256
=>k^2=16
=>k=4
=>AB=12cm; CB=20cm
b: BD là phân giác
=>AD/AB=CD/BC
=>AD/3=CD/5=(AD+CD)/(3+5)=16/8=2
=>AD=6cm; CD=10cm