Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
b: BFEC nội tiếp
=>góc HFE=góc HBC
=>góc HFE=góc HNM
=>FE//MN

a: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>BD//CH
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>CD//BH
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
b: BHCD là hình bình hành
nên BC cắt HD tại trung điểm của mỗi đường
=>I là trung điểm của HD
Xét ΔDAH có DI/DH=DO/DA
nen Io//AH và IO=AH/2
=>AH=2OI
c: G là trọng tâm
nên AG=2AI
Xét ΔAHD có
AI là trung tuyến
AG=2/3AI
DO đó: G là trọng tâm

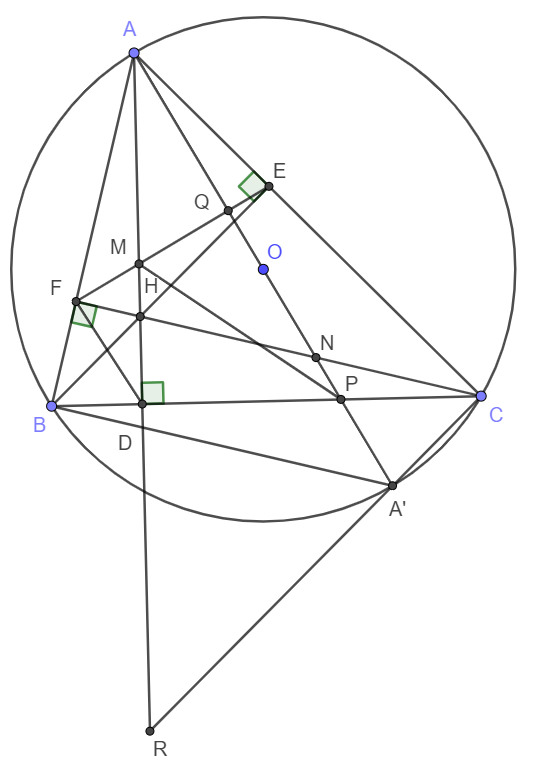
a) theo gt, BFC=BEC=90
=> BFEC nội tiếp (có 2 góc kề bang nhau)
góc AFC=ADC=90 => AFDC nội tiếp ( có 2 cạnh kề cùng nhìn một đoan thẳng bằng nhau)
b) vì tứ giác ABA'C nội tiếp => ABC = AA'C (cùng chắn cung AC)
Lại có ABC= AHF (Cùng phụ với góc BAD)
Ta thấy AFHE nội tiếp vì AFH +AEH = 90+90=180
=> AHF=AEF (Cùng chắn cung AF)
=>Đpcm
c) vì tứ giác EQA'C nôi tiếp
nên EQA'+ECA'=180 mà ECA'=90 vì là góc nội tiếp chắn nửa đường tròn
=> MQP=EQA'=90 ( vì MQP+EQA=180)
Trong đó ADC=90 =>Đpcm
d) Vì ABA'C VÀ FBDH nội tiếp nên góc NA'C=ABC=DHC
=>NA'C=DHC=>Đpcm