Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài giải:
Áp dụng các công thức:
\(Z_C=\dfrac{1}{\omega C}\text{= 50 Ω; }Z_L\text{= ωL = 20 Ω}\)
=> Z =\(\sqrt{R^2+\left(Z_L-Z_C\right)^2\text{= 30√2 Ω}}\)
Cường độ dòng điện hiệu dụng: I =\(\dfrac{U}{Z}=\dfrac{120}{30\sqrt{2}}=\dfrac{4}{30\sqrt{2}}\dfrac{4}{\sqrt{2}}A\)
Độ lệch pha: tanφ = \(\dfrac{Z_L-Z_C}{R}=-1\Rightarrow\varphi=-\dfrac{II}{4}\text{ }\) . Tức là i sớm pha hơn u một góc \(\dfrac{II}{4}\)
Vậy biểu thức tức thời của cường độ dòng điện là: i = 4cos(100πt +\(\dfrac{II}{4}\)) (A)
Áp dụng các công thức: ZC = 1ωC1ωC = 50 Ω; ZL = ωL = 20 Ω
=> Z = √R2+(ZL−ZC)2R2+(ZL−ZC)2 = 30√2 Ω
Cường độ dòng điện hiệu dụng: I = UZUZ = 12030√2120302 = 4√2A42A.
Độ lệch pha: tanφ = ZL−ZCRZL−ZCR = -1 => φ = −Π4−Π4. Tức là i sớm pha hơn u một góc Π4Π4.
Vậy biểu thức tức thời của cường độ dòng điện là: i = 4cos(100πt + Π4Π4) (A)
Ta có: R = 40Ω, C = 1/4000π F
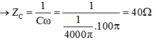
L = 0,1/π → ZL = Lω = 10Ω
Tổng quát:
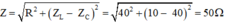
Điện áp hiệu dụng ở hai đầu AM:
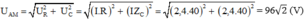
Cảm kháng: ZC = Lω = 30 Ω
Tổng trở: Z = √R2+Z2LR2+ZL2 = 30√2 Ω
Cường độ dòng điện hiệu dụng: I = UZUZ = 12030√2120302 = 4√242 A.
Độ lệch pha: tanφ = ZLRZLR = 1 => φ = +Π4+Π4. Tức là i trễ pha hơn u một góc Π4Π4.
Vậy biểu thức tức thời của cường độ dòng điện là: i = 4cos(100πt - Π4Π4) (A).
Chọn C
Áp dụng các công thức: Z C = 1 C ω = 50 Ω ; ZL = ωL = 20 Ω
⇒ Z = R 2 + ( Z L - Z C ) 2 = 30 2 Ω
Cường độ dòng điện hiệu dụng: I = U : Z = 120 : (30 2 ) = 4/ 2 A
Độ lệch pha: tanφ = Z L - Z C R = -1 => φ = π 4 . Tức là i sớm pha hơn u một góc π 4 .
Vậy biểu thức tức thời của cường độ dòng điện là: i = 4cos(100πt + π 4 ) (A)
Bài giải:
Hiện tượng cộng hưởng khi:
\(Z_L=Z_C\Leftrightarrow\omega L=\dfrac{1}{\omega C}\Rightarrow\omega=\sqrt{\dfrac{1}{LC}}=100\pi\left(\dfrac{rad}{s}\right)\)
Khi đó cường độ dòng điện hiệu dụng đạt giá trị cực đại và dòng điện cùng pha với điện áp:
\(I_{max}=\dfrac{U}{R}\dfrac{40\sqrt{2}}{20}=2\text{√}2A\) và \(\varphi=0\)
Biểu thức của dòng điện: i = 4cos(100πt) (A).
Hiện tượng cộng hưởng khi:
ZL = ZC⇔ ωL = 1ωC1ωC => ω = √1LC1LC = 100π (rad/s)
Khi đó cường độ dòng điện hiệu dụng đạt giá trị cực đại và dòng điện cùng pha với điện áp:
Imax = URUR = 40√22040220 = 2√2 A và φ = 0.
Biểu thức của dòng điện: i = 4cos(100πt) (A).
Ta có: R = 40Ω, C = 1/4000π F
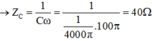
L = 0,1/π → ZL = Lω = 10Ω
Tổng quát:
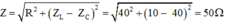
Biểu thức của i:
Ta có: u = 120√2cos100πt (V) → i = I0cos(100πt + φi)
Với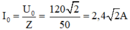 
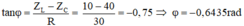
→ φ = φu – φi → φi = φu – φ = 0 – (- 0,6435) = 0,6435 rad
Vậy i = 2,4√2cos(100πt + 0,6435) (A)
Chọn D
Áp dụng các công thức: ZC = 1 C ω = 40 Ω; ZL = ωL = 10 Ω
=> Z = R 2 + ( Z L - Z C ) 2 = 50 Ω
Cường độ dòng điện hiệu dụng: I = U:Z = 120:50 = 2,4A.
Độ lệch pha: tan φ = Z L - Z C R = - 3 4 => φ ≈ -370 ≈ -0,645 rad. Tức là i sớm pha hơn u một góc 0,645 rad.
Vậy biểu thức tức thời của cường độ dòng điện là: i = 2,4 2 cos(100πt + 0,645 ) (A)
R = 30Ω, C = 1/5000π F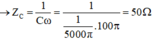 
L = 0,2/π H → ZL = Lω = 20Ω
Tổng trở: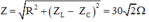 
Biểu thức của i:
Ta có: u = 120√2cos100πt (V) → i = I0cos(100πt + φi)
Với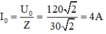 
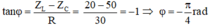
→ φ = φu – φi → φi = φu – φ = 0 – (-π/4) = π/4 rad
Vậy i = 4cos(100πt + π/4) (A)
Bài này thì có vẹo gì đâu bạn.
\(u=100\sqrt 2\cos(100\pi t)(V)\)
\(Z_L=\omega L = 10\Omega\)
\(Z_C=\dfrac{1}{\omega C}=20\Omega\)
Tổng trở \(Z=\sqrt{r^2+(Z_L-Z_C)^2}=10\sqrt 2 \Omega\)
\(\Rightarrow I_o=\dfrac{U_0}{Z}=10A\)
\(\tan\varphi=\dfrac{Z_L-Z_C}{R}=-1\Rightarrow \varphi=-\dfrac{\pi}{4}\)
Suy ra: \(\varphi=\dfrac{\pi}{4}\)
Vậy \(i=10\cos(100\pi t +\dfrac{\pi}{4})\) (A)
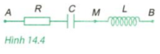
Bài giải:
Áp dụng công thức: \(Z_C\text{=40 Ω; Z_L}\text{= 10 Ω; Z = 50 Ω}\)
I = 2,4 A; tanφ =\(-\dfrac{3}{4}\) => φ ≈ \(-37^0\) ≈ -0,645 rad
a) i = 2,4√2cos(100πt - 0,645) (A).
B, \(U_{AM}=I\sqrt{R^2+Z^2_C}=\text{= 96√2 V}\)
Áp dụng các công thức: ZC = 40 Ω; ZL = 10 Ω; Z = 50 Ω
I = 2,4 A; tanφ =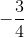
=> φ ≈ -370 ≈ -0,645 rad
a) i = 2,4√2cos(100πt - 0,645) (A).
b) UAM = I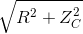
= 96√2 V