Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số hạt nhân chưa phóng xạ chính là số hạt nhân còn lại
\(N= N_0 2^{-\frac{t}{T}}= N_0 .2^{-4}= \frac{1}{16}N_0.\)

Số hạt nhân chưa bị phân rã (số hạt nhân còn lại)
\(N= N_0 2^{-\frac{t}{T}} = N_02^{-\frac{0,5T}{T}}= N_02^{-0,5}= \frac{N_0}{\sqrt{2}}.\)

Khối lượng Co bị phân rã là
\(\Delta m = m - m_0 = m_0 (1-2^{-\frac{t}{T}})\)
=> \(\frac{\Delta m }{m_0} = 1-2^{-\frac{1}{5,33}}= 0,122.\)
=> Sau 1 năm thì khối lượng Co bị phân rã chiếm 12,2 % khối lượng Co ban đầu.

Đáp án A
Phương pháp:
Áp dụng công thức tính khối lượng bị phâṇ rã sau phản ứng
![]()
Theo bài ra tra có:
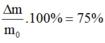
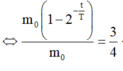
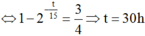

Khối lượng Rn còn lại sau 1,5 chu kì là: \(m=m_0.2^{-1,5}=2.2^{-1,5}(g)\)
Độ phóng xạ là: \(H=N.\lambda=\dfrac{2.2^{-1,5}}{222}.6,02.10^{23}.\dfrac{\ln 2}{3,8.24.3600}=...\)

Tỉ số giữa độ phóng xạ sau 11,4 ngày và độ phóng xạ ban đầu
\(\frac{H}{H_0}= 2^{-\frac{t}{T}}=2^{-\frac{11,4}{3,8}}= 0,125. \)
=> Độ phóng xạ sau 11,4 ngày chiếm 12,5 % độ phóng xạ ban đầu

\(H=H_02^{-\frac{t}{T}}\)
=> \(\frac{H}{H_0}=32^{-1}= 2^{-5}= 2^{-\frac{t}{T}}\)
=> \(t = 5T= 690.\)(ngày)

Số hạt nhân Natri là \(N_0 = nN_Á = \frac{m}{A}N_A\)
Độ phóng xạ ban đầu \(H_0 = \lambda N_0 = \frac{\ln 2}{T}\frac{m}{A}N_A= 6,73.10^{16}.(Bq)\)
Chú ý là trong khi tính độ phóng xạ theo đơn vị "Bq" thì chu kì phải đổi sang đơn vị "giây" .

Số hạt nhân ban đầu
\(N_0= \frac{H_0}{\lambda}\)
Khối lượng ứng cới độ phóng xạ \(H_0\) là
\(m_0 = nA= \frac{N_0}{N_A}A= \frac{H_0}{N_A}= \frac{5.3,7.10^{10}.14}{6,02.10^{23} \frac{\ln 2}{5570.365.24.3600}}= 1,09g.\)
Khối lượng chất phóng xạ đã bị phân rã là
\(\Delta m = m_0(1-2^{-\frac{t}{T}}) \)
=> \(\frac{\Delta m }{m_0}= 0,75 =1- 2^{-\frac{t}{T}}\)
=> \(t = -T\ln_20,25 = 30h.\)
D. 30h00'