Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: AE+EB=AB
BF+FC=BC
CG+GD=CD
DH+HA=DA
mà AB=BC=CD=DA và AE=BF=CG=DH
nên EB=FC=GD=HA
Xét ΔEAH vuông tại A và ΔGCF vuông tại C có
EA=GC
AH=CF
Do đó: ΔEAH=ΔGCF
=>EH=GF
Xét ΔEBF vuông tại B và ΔGDH vuông tại D có
EB=GD
BF=DH
Do đó: ΔEBF=ΔGDH
=>EF=GH
Xét ΔEAH vuông tại A và ΔFBE vuông tại B có
EA=FB
AH=BE
Do đó: ΔEAH=ΔFBE
=>EH=EF và \(\widehat{AEH}=\widehat{BFE}\)
\(\widehat{AEH}+\widehat{HEF}+\widehat{BEF}=180^0\)
=>\(\widehat{BFE}+\widehat{BEF}+\widehat{HEF}=180^0\)
=>\(\widehat{HEF}+90^0=180^0\)
=>\(\widehat{HEF}=90^0\)
Xét tứ giác EHGF có
EF=GH
EH=GF
Do đó: EHGF là hình bình hành
Hình bình hành EHGF có EF=EH
nên EHGF là hình thoi
Hình thoi EHGF có \(\widehat{HEF}=90^0\)
nên EHGF là hình vuông
b:
AH+HD=AD
=>AH+1=4
=>AH=3(cm)
ΔAEH vuông tại A
=>\(AE^2+AH^2=EH^2\)
=>\(EH^2=3^2+1^2=10\)
=>\(EH=\sqrt{10}\left(cm\right)\)
EHGF là hình vuông
=>\(S_{EHGF}=EH^2=10\left(cm^2\right)\)

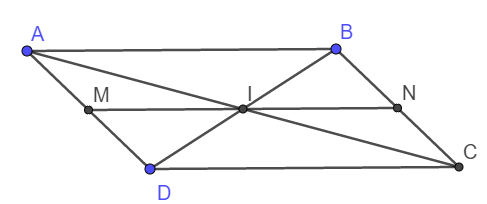
1. Xét tam giác ABD có MI // AB nên theo định lý Talet ta có:
\(\frac{MI}{AB}=\frac{DI}{DB}\)
Xét tam giác ABC có NI // AB nên theo định lý Talet ta có:
\(\frac{NI}{AB}=\frac{NC}{BC}\)
2. Xét tam giác BDC có IN // DC nên \(\frac{DI}{DB}=\frac{NC}{BC}\)
Từ đó ta có: \(\frac{MI}{AB}=\frac{NI}{AB}\Rightarrow MI=IN\)
Vậy I là trung điểm MN (đpcm)