Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

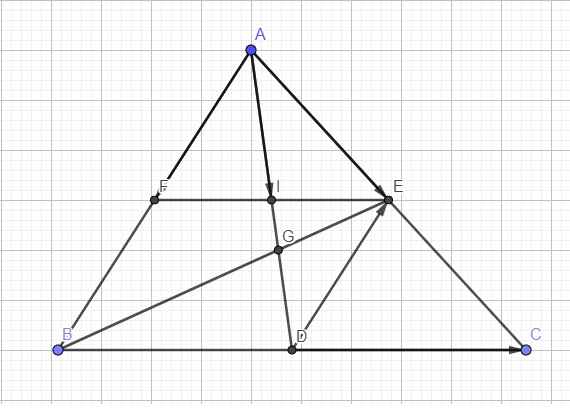
F là trung điểm AB \(\Rightarrow\overrightarrow{AF}=\dfrac{1}{2}\overrightarrow{AB}\) ; E là trung điểm AC \(\Rightarrow\overrightarrow{AE}=\dfrac{1}{2}\overrightarrow{AC}\)
Ta có EF song song BC (đường trung bình)
Mà D là trung điểm BC \(\Rightarrow\) I là trung điểm EF \(\Rightarrow AI\) là trung tuyến tam giác AEF
\(\Rightarrow\overrightarrow{AI}=\dfrac{1}{2}\overrightarrow{AE}+\dfrac{1}{2}\overrightarrow{AF}\)
Theo tính chất trọng tâm:
\(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AD}=\dfrac{2}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=\dfrac{2}{3}\left(\overrightarrow{AE}+\overrightarrow{AF}\right)=\dfrac{2}{3}\overrightarrow{AE}+\dfrac{2}{3}\overrightarrow{AF}\)
DE là đường trung bình tam giác ABC
\(\Rightarrow\overrightarrow{DE}=\dfrac{1}{2}\overrightarrow{BA}=-\dfrac{1}{2}\overrightarrow{AB}=-\overrightarrow{AE}\) hay \(\overrightarrow{DE}=-\overrightarrow{AE}+0.\overrightarrow{AF}\)
D là trung điểm BC \(\Rightarrow\overrightarrow{DC}=\dfrac{1}{2}\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{DC}=\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{AC}=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}=-\overrightarrow{AE}+\overrightarrow{AF}\)

a: \(\overrightarrow{AI}=\dfrac{1}{2}\left(\overrightarrow{AM}+\overrightarrow{AN}\right)=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\)

\(\overrightarrow{AF}=2\overrightarrow{FC}\Rightarrow\overrightarrow{AF}=\frac{2}{3}\overrightarrow{AC}\)
\(\overrightarrow{AM}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}\)
\(\overrightarrow{EI}=\frac{3}{4}\overrightarrow{IF}=\frac{3}{4}\left(\overrightarrow{IE}+\overrightarrow{EF}\right)\Rightarrow\overrightarrow{EI}=\frac{3}{7}\overrightarrow{EF}\)
\(\overrightarrow{AI}=\overrightarrow{AE}+\overrightarrow{EI}=\overrightarrow{AE}+\frac{3}{7}\overrightarrow{EF}=\overrightarrow{AE}+\frac{3}{7}\left(\overrightarrow{EA}+\overrightarrow{AF}\right)=\frac{4}{7}\overrightarrow{AE}+\frac{3}{7}\overrightarrow{EF}\)
\(\overrightarrow{AI}=\frac{4}{7}.\frac{1}{2}\overrightarrow{AB}+\frac{3}{7}.\frac{2}{3}\overrightarrow{AC}=\frac{2}{7}\overrightarrow{AB}+\frac{2}{7}\overrightarrow{AC}=\frac{4}{7}\left(\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}\right)=\frac{4}{7}\overrightarrow{AM}\)
\(\Rightarrow A;M;I\) thẳng hàng

\(\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AD}\)(D là trung điểm của BC) (1)
\(\overrightarrow{AM}+\overrightarrow{AN}=2\overrightarrow{AK}\)(K là trung điểm của MN) (2)
Lấy (1) trừ (2) có: \(\left(\overrightarrow{AB}+\overrightarrow{AC}\right)-\left(\overrightarrow{AM}+\overrightarrow{AN}\right)=2\left(\overrightarrow{AD}-\overrightarrow{AK}\right)\)
⇔\(\dfrac{\left(\overrightarrow{AB}+\overrightarrow{AC}\right)-\left(\overrightarrow{AM}+\overrightarrow{AN}\right)}{2}\)=\(\overrightarrow{KD}\)
⇔\(\dfrac{\left(\overrightarrow{AB}+\overrightarrow{AC}\right)-\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\right)}{2}\)=\(\overrightarrow{KD}\)
⇔\(\dfrac{\overrightarrow{AB}+\overrightarrow{AC}-\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{3}\overrightarrow{AC}}{2}\)=\(\overrightarrow{KD}\)
⇔\(\dfrac{\dfrac{1}{2}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}}{2}\)=\(\overrightarrow{KD}\)
⇔\(\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)=\(\overrightarrow{KD}\)

\(3BM=7CM=7\left(BC-BM\right)\Rightarrow10BM=7BC\)
\(\Rightarrow BM=\dfrac{7}{10}BC\Rightarrow\overrightarrow{BM}=\dfrac{7}{10}\overrightarrow{BC}\)
Ta có:
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{AB}+\dfrac{7}{10}\overrightarrow{BC}=\overrightarrow{AB}+\dfrac{7}{10}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)=\overrightarrow{AB}-\dfrac{7}{10}\overrightarrow{AB}+\dfrac{7}{10}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{AM}=\dfrac{3}{10}\overrightarrow{AB}+\dfrac{7}{10}\overrightarrow{AC}\)
Lời giải:
Theo đề thì $\overrightarrow{3BM}=7\overrightarrow{MC}=-7\overrightarrow{CM}$
Lại có:
$\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}$
$\Rightarrow 3\overrightarrow{AM}=3\overrightarrow{AB}+3\overrightarrow{BM}=3\overrightarrow{AB}-7\overrightarrow{CM}(1)$
$\overrightarrow{AM}=\overrightarrow{AC}+\overrightarrow{CM}$
$\Rightarrow 7\overrightarrow{AM}=7\overrightarrow{AC}+7\overrightarrow{CM}(2)$
Từ $(1);(2)\Rightarrow 10\overrightarrow{AM}=3\overrightarrow{AB}+7\overrightarrow{AC}$
$\Rightarrow \overrightarrow{AM}=\frac{3}{10}\overrightarrow{AB}+\frac{7}{10}\overrightarrow{AC}$

\(\overrightarrow{BM}=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\)

\(\overrightarrow{BM}=\dfrac{\overrightarrow{BA}+\overrightarrow{BC}}{2}=\dfrac{\overrightarrow{BA}+\overrightarrow{BA}+\overrightarrow{AC}}{2}=-\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\)
\(\overrightarrow{AN}=\overrightarrow{AB}+\overrightarrow{BN}=\overrightarrow{AB}+\dfrac{2}{5}\overrightarrow{BA}+\dfrac{2}{5}\overrightarrow{AC}=\dfrac{3}{5}\overrightarrow{AB}+\dfrac{2}{5}\overrightarrow{AC}\)