Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Em tham khảo tại link dưới đây nhé.
Câu hỏi của Nguyễn Thị Ngọc Ánh - Toán lớp 7 - Học toán với OnlineMath

Em tham khảo tại link dưới đây nhé.
Câu hỏi của Nguyễn Thị Ngọc Ánh - Toán lớp 7 - Học toán với OnlineMath

Em tham khảo tại link dưới đây nhé.
Câu hỏi của Nguyễn Thị Ngọc Ánh - Toán lớp 7 - Học toán với OnlineMath

a,Xét tg BAD và tg CEI
Có : CE=BD( gt)
Mà : AC=AB (1)
Và : AC=CI(2)
Từ (1)(2) =>AB=CI
Mà : B=C(tg cân)(3)
Và : goc ACD= góc ICE(đđ)(4)
Từ (3) và (4) => góc ICE= góc ADB
Nên : tg ABD=tgICE (cgc)
Vậy đpcm
b, Xét tg ABC
Theo định lý pi-ta-go có :
BC2=AB2+AC2 (1)
Xét tg ADE
Theo định lý P-i-ta-go có :
DE2=AE2+AD2 (2)
Từ (1) và (2) suy ra :
(BC2=AB2+AC2)= (DE2=AE2+AD2)
Vây : đpcm
Câu 2 :ko bt
Câu 3 :ko bt
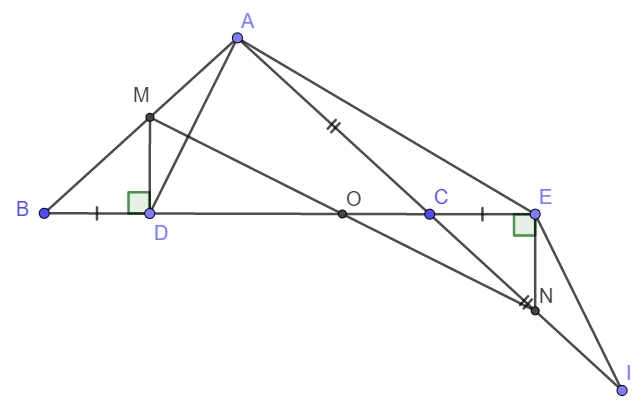
Hình nek
A B C D E I M N
Ai giải dược mik k cho
Còn ai ko giải thì next giùm :))))))

1)
+) Ta thấy \(\widehat{ECI}=\widehat{ACB}\) (Hai góc đối đỉnh)
Mà \(\widehat{ACB}=\widehat{ABC}\) (Tam giác ABC cân tại A)
nên \(\widehat{ECI}=\widehat{DBA}\)
Xét tam giác ABD và tam giác ICE có:
BD = CE (gt)
\(\widehat{DBA}=\widehat{ECI}\left(cmt\right)\)
CI = BA ( Cùng bằng AC)
\(\Rightarrow\Delta ABD=\Delta ICE\left(c-g-c\right)\)
+) Xét tam giác AEI, theo bất đẳng thức trong tam giác, ta có:
AI > AE + EI
Lại có do \(\Delta ABD=\Delta ICE\Rightarrow AD=IE\)
Vậy nên ta có AI > AE + AD \(\Rightarrow2AC>AD+AE\Rightarrow AB+AC>AD+AE\)
2) Do \(\Delta ABD=\Delta ICE\Rightarrow\widehat{MBD}=\widehat{NCE}\)
Vậy thì ta thấy ngay \(\Delta BDM=\Delta CEN\) (Cạnh góc vuông - góc nhọn kề)
\(\Rightarrow BM=CN\)
3) Ta thấy AB + AC = AM + MB + AC = AM + CN + AC = AM + AN
Ta cần chứng minh BC < MN.
Do BD = EC nên AC = DE
Xét tam giác vuông MDO ta có DO < MO (Quan hệ đường vuông góc, đường xiên)
Ta cũng có OE < ON
Vậy nên DE < MN hay BC < MN
Từ đó: AB + AC + BC < AM + AN + MN
Hay \(P_{AMN}>P_{ABC}\)
- Gợi ý:
Câu 1:
a) - Sửa lại đề: Tam giác ABD=Tam giác ICE (c-g-c) do có AB=AC=CI, góc ABC=góc ACB=góc ECI, BD=CE.
b) Do tam giác ABD=Tam giác ICE nên AD=IE :
AE+EI>AI=2AC=AB+AC
=>AE+AD>AB+AC.
Câu 2:
- Tam giác MBD=Tam giác NCE do góc MDB=góc CEN=900, BD=CE,
góc MBD=góc NCE. nên BM=CN
Câu 3:
- AB=AM+BM ; CI=CN+NI.
=>AM=NI.
=>AM+AN=AM+NI=AI=AB+AC.
-c/m MN>BC (c/m mệt lắm nên mình nói ngắn gọn).
MN cắt BC tại F =>MF>DF, NF>EF
MF+NF>DF+EF=DF+CF+CE=DF+CF+BD=BC =>MN>BC
cảm ơn bạn nhiều !