Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vẽ đồ thị biểu diễn sự phụ thuộc của ε vào σ
Chọn tỉ lệ vẽ trên các trục tọa độ:
- Trục hoành: 1 cm → σ = 0,5. 10 8 N/ m 2
- Trục tung: 1 cm → ε = 0,2. 10 - 3
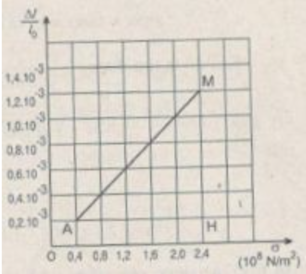
Đồ thị có dạng đường thẳng chứng tỏ độ biến dạng tỉ đối Δl/l0 của thanh sắt tỉ lệ thuận với ứng suất σ của lực kéo tác dụng lên thanh sắt, nghĩa là:
ε = ∆ l/ l 0 = a ε
Hệ số tỉ lệ a được xác định bởi hệ số góc của đường biểu diễn đồ thị:
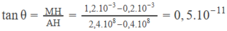

Tìm giá trị của suất đàn hồi E và hệ số đàn hồi k của thanh sắt.
![]()
Từ đó tìm đươc suất đàn hồi :
![]()
và hệ số đàn hồi:
![]()

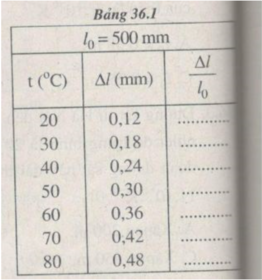
Kết quả tính độ dãn dài tỉ đối của thanh thép ở những nhiệt độ t khác nhau (được ghi ở bảng bên)
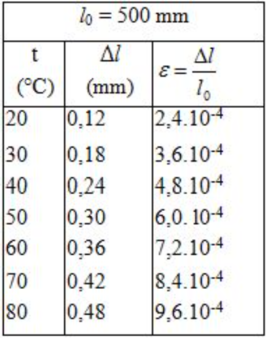

Chọn tỉ xích trên các trục toạ độ :
Trục hoành : 1 cm → t = 10 ° C.
Trục tung : 1 cm → = 1,2. 10 - 4
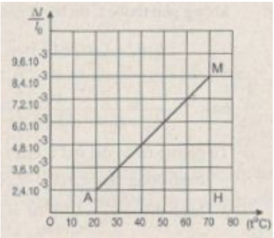
Đường biểu diễn đồ thị vẽ được trên

Vì hai bức tường cố định nên khoảng cách giữa chúng không đổi. Khi nhiệt độ tăng thì thanh xà nở dài thêm một đoạn ∆ l = 1,2 mm. Do đó, thanh xà tác dụng lên hai bức tường một lực có cường độ tính theo định luật Húc :
![]()

Bài 1:
\(\alpha= 0\) \(\Rightarrow F = F_1+F_2 = 16+12=28N\)
\(\alpha = 30^0\)\(\Rightarrow F^2=16^2+12^2+2.16.12.\cos30^0=...\Rightarrow F\)
Các trường hợp khác bạn tự tính nhé.
Bài 2:
Ta có: \(F_1=k.\Delta \ell_1=k.(0,24-0,12)=0,12.k=5\) (1)
\(F_1=k.\Delta \ell_2=k.(\ell-0,12)=10\) (2)
Lấy (2) chia (1) vế với vế: \(\dfrac{\ell-0,12}{0,12}=2\)
\(\Rightarrow \ell = 0,36m = 36cm\)
Bài 3:
Áp lực lên sàn: \(N=P=mg\)
Áp dụng định luật II Niu tơn ta có: \(F=m.a\Rightarrow -F_{ms}=ma\)
\(\Rightarrow a = \dfrac{-F_{ms}}{m}= \dfrac{-\mu.N}{m}== \dfrac{-\mu.mg}{m}=-\mu .g =- 0,1.10=-1\)(m/s2)
Quãng đường vật đi được đến khi dừng lại là \(S\)
Áp dụng công thức độc lập: \(v^2-v_0^2=2.a.S\)
\(\Rightarrow 0^2-10^2=2.1.S\Rightarrow S = 50m\)
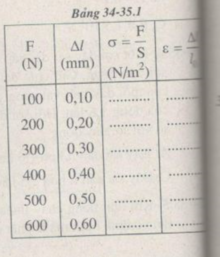
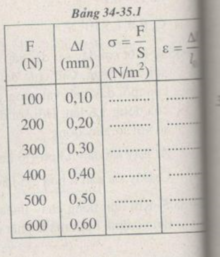
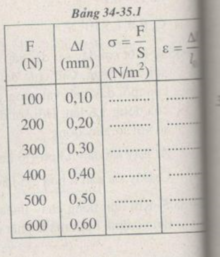
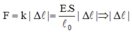
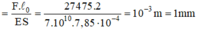
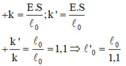
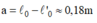
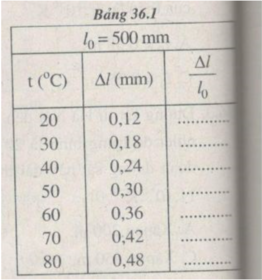
Tính độ dãn dài tỉ đối ε của thanh sắt và ứng suất σ của lực kéo tác dụng lên thanh sắt trong mỗi lần đo.