Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kết quả tính độ dãn dài tỉ đối của thanh thép ở những nhiệt độ t khác nhau (được ghi ở bảng bên)
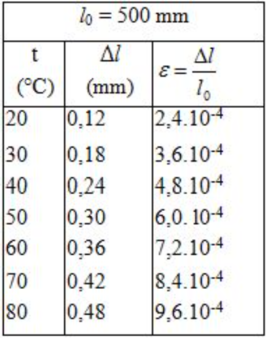

Hình 36.1G có dạng đoạn thẳng.
Điều này chứng tỏ độ biến dạng tỉ đối ∆ l/ l 0 của thanh sắt tỉ lệ thuận với độ tăng nhiệt độ t (tính từ 0 ° C):
∆ l/ l 0 = α t
Nhận xét thấy hệ số tỉ lệ α chính là hệ số nở dài của thép.
Hệ số tỉ lệ α được xác định bởi hệ số góc của đường biểu diễn đồ thị ở Hình 36.1G.

B3: to = 20C
\(\Delta l=l_o\alpha\left(50-20\right)=0,0033m\)
=> phải để hở 1 khe lớn hơn hoặc = 0,0033m
B1: a, \(\Delta l=l_o\alpha\left(40-20\right)=0,00033m\)
b, \(l=\Delta l+l_o=1,50033m\)
B5: Ta co: \(V=V_o\left[1+3\alpha\left(t-t_o\right)\right]\)
=> \(\frac{m}{D}=\frac{m}{D_o}\left[1+3\alpha\left(500-0\right)\right]\)
=> D \(\approx6885,4\)
B2: \(l-l_o=l_o\alpha\left(t-0\right)\)
=> \(l_o\alpha\left(t-0\right)=0,0008\)
=> \(t\approx72,7^oC\)

Tóm tắt :
Thép Nước
m1 = 5kg V2 = 3 lít = m2 = 3 kg
t1 = 345oC t2 = 30oC
t2 = 30oC c2 = 4200 J/kg.K
c1 = 460 J/kg.K t1 = ?
Giải
Nhiệt lượng của miếng thép tỏa ra là
\(Q_{tỏa}=m_1.c_1.\left(t_1-t_2\right)=5.460.\left(345-30\right)=724500\left(J\right)\)
Ta có : Qtỏa = Qthu
\(\Rightarrow m_2.c_2.\left(t_2-t_1\right)=724500\left(J\right)\\ \Rightarrow\Delta t=\dfrac{724500:4200}{3}=57,5^oC\\ \Rightarrow-t_1=30-57,5\\ \Rightarrow t_1=27,5^oC\)

Sorry nha mình tính lộn
Thể tích của lượng khí đó ở 546oC khi áp suất không đổi là 20lít.
Đây là quá trình đẳng áp =>Áp dụng định luật Gay Luy-xac ta có:
V1T1=V2T2=>V2=T2.V1T1=(546+273).10273+273=15litV1T1=V2T2=>V2=T2.V1T1=(546+273).10273+273=15lit
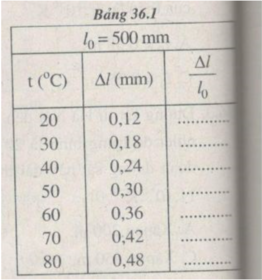
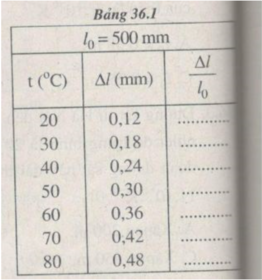
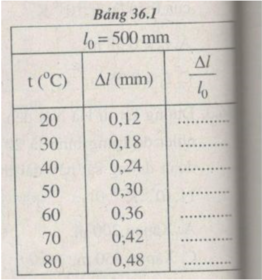
Chọn tỉ xích trên các trục toạ độ :
Trục hoành : 1 cm → t = 10 ° C.
Trục tung : 1 cm → = 1,2. 10 - 4
Đường biểu diễn đồ thị vẽ được trên