Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
A B C D Cả 4 câu đều là 1 hình như thế này, chỉ có kí hiệu khác nhau, bạn tự dựa vào nội dung câu hỏi mà kí hiệu lên hình nhé.
Câu 1:
Xét tam giác ABD và tam giác ACD:
ADB= ADC =90o
AD chung
DB= DC
=> tam giác ABD = tam giác ACD (2 cạnh góc vuông)
=> góc B = góc C (2 góc tương ứng)
Vậy tam giác ABC cân
Câu 2:
Chứng minh y chang câu 1
Câu 3:
Xét tam giác ABD và tam giác ACD:
ADB= ADC =90o
AD chung
BAD = CAD
=> tam giác ABD = tam giác ACD (cạnh góc vuông_ góc nhọn)
=> góc B = góc C (2 góc tương ứng)
Vậy tam giác ABC cân
Câu 4:
Chứng minh giống hệt câu 3.
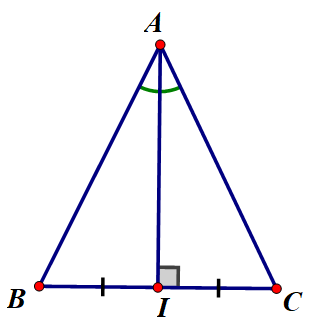
Trong một tam giác cân đường cao vừa là đường trung tuyến vừa và đường phân giác.
Xét tam giác ABC có AI là đường trung trực vừa là đường phân giác
vì AI là đường trung trực nên AI vuông góc với BC và I là trung điểm cuả BC
xét 2 tam giác vuông ABI và tam giác vuông ACI có;
IA chung
góc BAI=gócCAI (do AI là phân giác)
do đó tam giác BAI =tam giác CAI
suy ra AB=AC (2 cạnh tương ứng)
suy ra tam giác ABC cân tại A (định nghĩa tam giác cân)
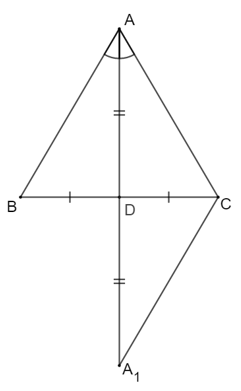
- Giả sử AD vừa là đường trung tuyến, vừa là đường phân giác của tam giác ABC.
Ta cần chứng minh ∆ABC cân tại A.
Kéo dài AD một đoạn DA1 sao cho DA1 = AD.
- ∆ADB và ∆A1DC có
AD = DA1 (cách vẽ)
BD = CD (do D là trung điểm BC)
⇒ ∆ADB = ∆A1DC (c.g.c)
⇒ 
(hai góc tương ứng), AB = A1C (hai cạnh tương ứng) (1)
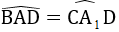
⇒ ∆ACA1 cân tại C ⇒ AC = A1C (2)
Từ (1) và (2) ⇒ AB = AC.
Vậy ∆ABC cân tại A
Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân.
HOK T ~
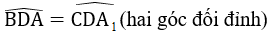
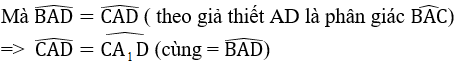
phải, vì trong tam giác cân đường cao ứng với cạnh đáy dồng thời là đường trung tuyến, phân giác và trung trực