Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải
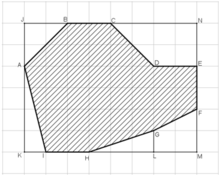
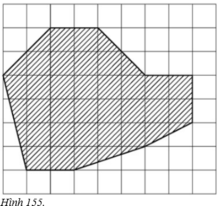
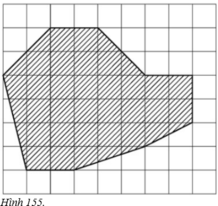
Diện tích hình chữ nhật JKMN là: 8.6 = 48 (cm2)
Diện tích tam giác vuông JAB là: JA.JB/2 = 2.2/2 = 2 (cm2).
Diện tích tam giác vuông AKI là: AK.KI/2 = 2 (cm2).
Diện tích tam giác vuông HLG là: HL.LG/2 = 1,5 (cm2).
Diện tích hình thang vuông GLMF là:
\(\frac{\left(GL+FM\right).LM}{2}=\frac{\left(1+2\right).2}{2}=3\left(cm^2\right)\)
Diện tích hình thang vuông CDEN là:
\(\frac{\left(CN+DE\right).EN}{2}=\frac{\left(2+4\right).2}{2}=6\left(cm^2\right)\)
Vậy diện tích của hồ nước trên bản đồ là:
SABCDEFGHI = SJKML – SAJB – SAKI – SHLG – SGLMF – SCDEN
= 48 – 2 – 2 – 1,5 – 3 – 6
= 33,5 (cm2).
Bản đồ tỉ lệ 1 : 10 000 nên diện tích thực của hồ là:
33,5.10 000 = 335 000 (cm2) = 33,5 m2.

Diện tích hình chữ nhật JKMN là: 8.6 = 48 (cm2)
Diện tích tam giác vuông JAB là: JA.JB/2 = 2.2/2 = 2 (cm2).
Diện tích tam giác vuông AKI là: AK.KI/2 = 2 (cm2).
Diện tích tam giác vuông HLG là: HL.LG/2 = 1,5 (cm2).
Diện tích hình thang vuông GLMF là:
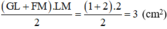
Diện tích hình thang vuông CDEN là:
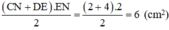
Vậy diện tích của hồ nước trên bản đồ là:
SABCDEFGHI = SJKML – SAJB – SAKI – SHLG – SGLMF – SCDEN
= 48 – 2 – 2 – 1,5 – 3 – 6
= 33,5 (cm2).
Bản đồ tỉ lệ 1 : 10 000 nên diện tích thực của hồ là:
33,5.(10000)2 = 33,5.108 (cm2) = 33,5 (ha)
(Lưu ý: tỉ lệ 1 : 10 000 tức là 1cm trên bản đồ ứng với 10 000cm trên thực tế. Suy ra, 1cm2 trên bản đồ ứng với (10 000)2 cm2 trên thực tế)

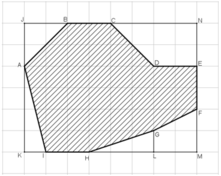
Diện tích hình chữ nhật JKMN là: 8.6 = 48 (cm2)
Diện tích tam giác vuông JAB là: JA.JB/2 = 2.2/2 = 2 (cm2).
Diện tích tam giác vuông AKI là: AK.KI/2 = 2 (cm2).
Diện tích tam giác vuông HLG là: HL.LG/2 = 1,5 (cm2).
Diện tích hình thang vuông GLMF là:
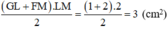
Diện tích hình thang vuông CDEN là:
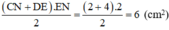
Vậy diện tích của hồ nước trên bản đồ là:
SABCDEFGHI = SJKML – SAJB – SAKI – SHLG – SGLMF – SCDEN
= 48 – 2 – 2 – 1,5 – 3 – 6
= 33,5 (cm2).
Bản đồ tỉ lệ 1 : 10 000 nên diện tích thực của hồ là:
33,5.10 000 = 335 000 (cm2) = 33,5 m2.

a,
Đặt: \(\hept{\begin{cases}\frac{a^2+b^2-c^2}{2ab}=x\\\frac{b^2+c^2-a^2}{2bc}=y\\\frac{c^2+a^2-b^2}{2ac}=z\end{cases}}\)
a, Ta chứng minh \(x+y+z>1\)hay \(x+y+z-1>0\left(1\right)\)
Ta có BĐT \(\left(1\right)\Leftrightarrow\left(x+1\right)+\left(y-1\right)+\left(z-1\right)>0\left(2\right)\)
Ta có: \(x+1=\frac{a^2+b^2-c^2}{2ab}+1=\frac{\left(a+b\right)^2-c^2}{2ab}=\frac{\left(a+b-c\right)\left(a+b+c\right)}{2ab}\)
Và: \(y-1=\frac{b^2+c^2-a^2}{2bc}-1=\frac{\left(b-c\right)^2-a^2}{2bc}=\frac{\left(b-c-a\right)\left(b-c+a\right)}{2bc}\)
Và: \(z-1=\frac{c^2+a^2-b^2}{2ac}-1=\frac{\left(c-a\right)^2-b^2}{2ac}=\frac{\left(c-a-b\right)\left(c-a+b\right)}{2ac}\)
\(\left(2\right)\Leftrightarrow\left(a+b-c\right)\left[\frac{c\left(a+b+c\right)+a\left(b-c-a\right)-b\left(c-a+b\right)}{2abc}\right]>0\)
\(\Leftrightarrow\left(a+b-c\right)\left[c^2-\left(a-b\right)^2\right]>0\left(abc>0\right)\)
\(\Leftrightarrow\left(a+b-c\right)\left(a-b+c\right)\left(-a+b+c\right)>0\)
BĐT cuối đúng vì \(a,b,c\)thỏa mãn \(BĐT\Delta\left(đpcm\right)\)
b, Để \(A=1\Leftrightarrow\left(z+1\right)+\left(y-1\right)+\left(z-1\right)=0\)
\(\Leftrightarrow\left(a+b-c\right)\left(a-b+c\right)\left(-a+b+c\right)=0\)
Từ trên ta suy ra được 3 trường hợp:
- Trường hợp 1: \(a+b-c=0\Rightarrow\hept{\begin{cases}x+1=0\\y-1=0\\z-1=0\end{cases}}\hept{\Rightarrow\begin{cases}x=-1\\y=-1\\z=1\end{cases}}\)
- Trường hợp 2:\(a-b+c=0\Rightarrow\hept{\begin{cases}x-1=\frac{\left(a-b-c\right)\left(a-b+c\right)}{2ab}=0\\y-1=0\\z+1=\frac{\left(c+a-b\right)\left(c+a+b\right)}{2ca}\end{cases}}\Rightarrow\hept{\begin{cases}x=1\\y=1\\z=-1\end{cases}}\)
- Trường hợp 3: \(-a+b+c=0\Rightarrow\hept{\begin{cases}x-1=0\\y+1=\frac{\left(b+c-a\right)\left(b+c+a\right)}{2bc}\\z-1=0\end{cases}\Rightarrow\hept{\begin{cases}x=1\\y=-1\\z=1\end{cases}}}\)
Từ các trường trên ta thấy trường hợp nào cũng có 2 trong 3 phân thức \(x,y,z=1\)và còn lại \(=-1\)
1cm trên bản đồ = 200000 cm trên thực tế
200000cm
t.i.c.k nha