Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

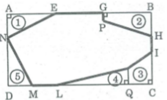
Giả sử hình chữ nhật là ABCD.
Trên AB, 2 giao điểm là E và G.
Trên BC hai giao điểm là I và H.
Trên CD hai giao điểm là L và M. Giao điểm trên AD là N. Hình thang tại đỉnh B có giao điểm là P, điểm trên đường gấp khúc IL là K.
Kẻ KQ ⊥ CD, gọi điện tích phẩn gạch đậm là S.
Ta có: S = S A B C - S A N E - S B H P G - S I C Q K - S D M N
Dùng thước chia khoảng đo các đoạn (mm):
AB, AD, AE, AN, PG, GB, BH, IC, CQ, QK, LQ, DM


Theo giả thiết, ta có:
\(\Delta ABC \backsim\Delta MNP\) theo hệ số tỉ lệ là \(\frac{1}{{1\,000\,000}}\)
\(\Delta A'B'C' \backsim\Delta MNP\) theo hệ số tỉ lệ là \(\frac{1}{{1\,500\,000}}\).
Từ đó ta có:
\(\begin{array}{l}\frac{{AB}}{{MN}} = \frac{{BC}}{{NP}} = \frac{{CA}}{{PM}} = 1\,000\,000\\ \Rightarrow AB = 1\,000\,000MN,\,\,BC = 1\,000\,000NP,\,\,CA = 1\,000\,000PM\end{array}\)
và \(\begin{array}{l}\frac{{A'B'}}{{MN}} = \frac{{B'C'}}{{NP}} = \frac{{C'A'}}{{PM}} = 1\,500\,000\\ \Rightarrow A'B' = 1\,500\,000MN,\,\,B'C' = 1\,500\,000NP,\,\,C'A' = 1\,500\,000PM\end{array}\)
Ta thấy
\(\begin{array}{l}\frac{{AB}}{{A'B'}} = \frac{{1\,000\,000MN}}{{1\,500\,000MN}} = \frac{2}{3}\\\frac{{BC}}{{B'C'}} = \frac{{1\,000\,000NP}}{{1\,500\,000NP}} = \frac{2}{3}\\\frac{{CA}}{{C'A'}} = \frac{{1\,000\,000PM}}{{1\,500\,000PM}} = \frac{2}{3}\\ \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{CA}}{{C'A'}}\end{array}\)
\( \Rightarrow \Delta ABC \backsim\Delta A'B'C'\) (c-c-c) với tỉ số đồng dạng là \(\frac{2}{3}\).
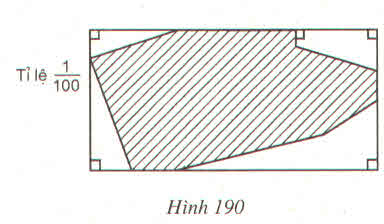

100.000x10=1.000.000(cm)
=10(km)