Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Theo giả thiết, ta có: mOx+aOx=180 độ (do ox là tia nằm giữ của góc mOa nên suy ra)
và mOx-aOx=20 độ
suy ra: mOx=(180+20):2=100 độ
aOx= mOx-20=100-20=80 độ
b)Do Ob là tia phân giác của của góc aOx nên:
bOx=aOx/2=80/2=40 độ
Ta có Oc vuông góc với Ob tại O nên suy ra góc bOc bằng 90 độ
=> cOx+bOx=bOc
hay cOx+40 = 90
=> cOx= 50 độ
c) Ta có: cOx+mOc=mOx
hay 50+mOc=100
=> mOc=50 độ
Do đó mOc=cOx (=50 độ) => Oc là tia phân giác của mOx

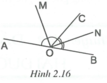
Ta có O M ⊥ O N ⇒ M O N ^ = 90 ° .
Tia OM là tia phân giác của góc AOC nên A O M ^ = M O C ^ .
Tia ON là tia phân giác của góc BOC nên B O N ^ = N O C ^ .
Xét tổng
A O C ^ + B O C ^ = 2 M O C ^ + 2 N O C ^ = 2 M O C ^ + N O C ^ = 2 M O N ^ = 2.90 ° = 180 ° .
Hai góc kề AOC và BOC có tổng bằng nên hai tia OA, OB đối nhau.
Đường trung trực – Hai góc có cạnh tương ứng vuông góc

Ta có:\(\widehat{AOC}+\widehat{COD}=90độ\)
\(30độ+\widehat{COD}=90độ\)
\(\widehat{COD}=90độ-30độ\)
\(\widehat{COD}=60độ\)
Ta có:\(\widehat{COB}+\widehat{BOD}=90độ\)
\(60độ+\widehat{BOD}=90độ\)
\(\widehat{BOD}=90độ-60độ\)
\(\widehat{BOD}=30độ\)

Ta có:
OC nằm giữa OA và OB
\(\widehat{AOC}+\widehat{COB}=\widehat{AOB}\)
Ta lại có:
\(30^o+\widehat{COB}=120^o\)
\(\Rightarrow\widehat{COB}=120^o-30^o\)
\(\widehat{COB}=90^o\)
\(\Rightarrow OB\perp OC\)
=> ĐPCM

Đầu tiên bạn phải kẻ hình : Có 2 mút là C và B , O nằm giữa C và B . Điểm A nằm giữa B và O
Oa , Vì 4 điểm A , B , C , O đều nằm trên 1 tia
=> 4 điểm A , B , C , O thẳng hàng
Vậy 4 điểm A , B , C , D thẳng hàng
b , Vì 2 tia OA và OC là 2 tia đối nhau
đầu tiien bạn phải kẻ hình: có 2 mút là c và b, o nằm giữa c và b. điểm a nằm giữa c và o.
a) vì 4 điểm A,B,C,O cùng nằm trên 1 tia.
=> 4 điểm A,B,C,O thẳng hàng.
Vậy 4 điểm A,B,C,O thẳng hàng.
b) Vì tia OA và tia Ob là 2 tia đối nhau.
=> điểm Onằm giữa A và B.
=> Điểm A không nằm giữa O và B.
Vậy điểm A không nằm giữa O và B.
Theo đề ra, ta có:
\(MOC=NOC\)
\(\Rightarrow OC\)nằm giữa \(OM\)và \(ON\)
\(MOA=MOB\)
\(\Rightarrow OM\)nằm giữa \(OA\)và \(OB\)